Beating Broker Margin
A survey of leverage available to the retail investor
Table of Contents
Are you a retail investor looking to multiply your stock purchasing power? Have ridiculously-high margin rates from your broker got you down? Whether you read my last article and you're convinced leverage is appropriate for you or you want to make more money from your surely well-researched Gamestop position, leverage, or the ability to scale exposure to certain securities beyond what's possible by simply buying and selling them, is an important tool allowing any investor to optimize any portfolio to better fit a desired level of risk.
The traditional way to add leverage is to borrow money "on the margin" – i.e., secured by the value of the account's positions – from one's broker. The problem is, interest rates on such loans available to retail investors are really, really bad. If these margin loans were the only way for retail to access leverage, this would induce retail investors seeking high returns to invest in risky assets even if not optimal when risk-adjusted, and it would rule out speculation on entire segments like fixed income and Forex markets (where price movements are relatively small). Luckily, it turns out that with knowledge of derivatives markets (and in some cases, level 4 options approval), retail investors can (implicitly) borrow at significantly lower rates. In this article, we'll use no-arbitrage pricing to motivate successively more intricate derivatives strategies for accessing leverage, compare this to how big institutions borrow money, and finally write some code that uses Yahoo finance data to determine these implied rates and show how they evolve over time.
Note: this article was posted at the same time as this one, and assumes you have read it and thus are familiar with the concept of no-arbitrage pricing. Also, this article is not intended as an apology of leveraged investing, nor does it provide advice on how much one should leverage a particular position; it merely discusses and compares several strategies available through the average retail brokerage for accessing it. Finally, all annualized returns quoted in this article will be in terms of APY/YTM (so annually compounded), and, if risky, normalized via geometric mean (to account for volatility), unless otherwise stated. I know this is not always standard practice in presenting e.g. bond yields, but I have more experience in equities than fixed income, and quoting equity returns in APY is standard practice1.
Margin (is expensive)
Even if you're not familiar with interest rates right now, the published margin rates of those brokers I linked above should obviously jump out as very high. In the case of Fidelity and Schwab, at the time of writing, their \(>13.5\%\) rates exceed essentially every other type of variable-rate secured credit by a wide margin, including prime adjustable-rate home mortgages, HELOCs, and variable-rate auto loans on new cars (loans on used cars seem roughly the same right now). Interactive brokers, who have by far the most competitive margin rate I'm aware of, is much better at 6.83%, but even this can be misleading, as it compounds daily (to be clear, so do Fidelity and Schwab, but the other secured credit types above are generally compounded monthly). That means you'd actually be paying \((1 + 0.0683/365)^{365} - 1 = 7.07 \%\) per year in compounding interest – very sneaky! To be fair, overnight rates like SOFR (I will explain what this is later, but for now just think of it as the canonical risk-free rate) are also usually published with respect to daily compounding, so 5.34% SOFR at the time of writing translates to \((1 + 0.0534/365)^{365} - 1 = 5.48 \%\) when annualized.
Putting aside nitpicks about compounding, this 159bp (basis points, meaning additive hundredths of a percent) gap between SOFR and the best broker margin rate for retail-sized accounts is still notably high – it generally exceeds historical credit spreads of most investment-grade bonds – especially considering the debt is secured by very liquid assets pre-approved by the lender (the broker) and can be called back, including via automated margin calls, at any time. Why do brokers charge such high rates for lending involving so little credit risk? It's clear that they're capable of more competitive rates – Interactive Brokers advertises rates just 52bp over SOFR on balances over $200 million. The only reasonable explanation seems to be that the market for margin at retail account sizes is uncompetitive, with brokers collecting a tidy spread from traders too small to negotiate.
Futures contracts
Luckily, retail brokers aren't the only market players offering collateralized leverage on investments – clearing houses provide an analogous service every day, on the same terms to institutions as retail traders, by guaranteeing futures contracts.
A futures contract is a contract in which a buyer (the long position) agrees to pay a seller (the short position) a specified amount of money (the "delivery price") to buy a specified amount2 of an underlying security on a specified date (the "delivery date"), regardless of what the actual price (the "spot price") is at that date. Or at least, that was how they used to work3 – now much of the financial industry trades in cash-settled ("regulated") futures, in which money is automatically transferred between the accounts of buyers and sellers by the clearing house according to whose position is profitable, without ever needing to trade in the underlying security. Generally, this is not only done at the delivery date of the contract, but happens in over the lifetime of the contract as the price of the underlying asset rises and falls ("marking-to-market"), such that the clearing house will have already assessed any gains or losses by the time a cash-settled contract expires. The clearing house can automatically (force brokers to) liquidate traders' positions to cover these obligations, and traders are required to have a specified amount of collateral (which is allowed to be in stocks, bonds, etc) for this purpose. Since futures contracts don't require any up-front cost from the buyer, only enough collateral to secure the position, the buyer of a futures contract seems to be receiving a similar product as margin from a broker. Yet clearing houses generally charge the same fees to institutional investors as they do to retail – that means whatever leverage we get from these contracts must be competitive, otherwise no institutional investors would trade them!
This intuition can easily be formalized by a no-arbitrage argument. Here, we'll refer to the price the contract appears to trade at on an exchange, which is not the up-front cost to enter a position, but the number the clearing house uses to credit/debit accounts, as the "delivery price", with the "price" being the ($0) up-front cost to enter a position. When a futures contract expires, the clearing house ensures that its delivery price is the same as the price of the underlying asset by transferring balance between accounts according to position sizes, so a replicating strategy for a futures contract is to simply purchase one unit of the underlying using money borrowed at the risk-free rate, which we will assume for the moment is constant, plus any cost (e.g. we would add storage costs for commodities and subtract dividends for indices) from holding the underlying, which we will assume for the moment are zero. This implies there is a unique arbitrage-free price – we already knew this, it's $0 – but more importantly, it tells us the current delivery price of a futures contract must equal the current price of the underlying plus the interest it costs to borrow this much. If the delivery price were any lower, institutions with access to the risk-free rate would buy the stock, lend the proceeds, and short the future, or vice versa if it were priced higher. In other words, buying a long futures contract and holding it until expiration is essentially the same as borrowing one unit of the underlying at the risk-free rate – that's exactly what we wanted to achieve with margin!
Unfortunately, the two assumptions that this argument rests upon don't reflect reality, and without them, pricing futures becomes much messier. First, we mentioned above that futures contracts are marked to market, meaning cash is transferred on a daily basis as one's position goes up and down. This means that the party with the winning position on a particular day can lend this extra cash at the risk-free rate, while the losing party loses out on this same amount of interest. If the overnight risk-free rate is constant, this doesn't matter for measures which are risk-neutral with respect to all times because the price of the underlying will, in expectation4, neither overperform nor underperform an investment at the risk-free rate at all times, so neither side of the contract is likelier to pay additional interest in expectation with respect to such measures, and such measures are what are used to price derivatives due to no-arbitrage constraints (this uses a more complicated version of what was proven in the companion article). However, if we consider the risk-free rate to be a random time series and assume that it is negatively correlated (with respect to a risk-neutral measure) with stock index returns, which has been accurate historically, we get that the long side of the future is likely to receive more money via marking to market when interest rates are lower, and vice versa, meaning the long side does not receive as much when investing this additional money and thus would prefer to buy the underlying with borrowed money as opposed to holding the future. Similarly, the short side is likelier to receive additional money via marking-to-market when interest rates are higher, so should prefer the futures contract to selling the underlying and lending the proceeds. The future should thus trade at a lower delivery price than that found by the calculation above.
Second, when companies issue dividends, their stock falls by the dividend amount on the ex-dividend date because this money is distributed to shareholders, so both capital and appreciation and dividends must be accounted for when constructing the risk-neutral measure with respect to stock returns. But futures holders aren't entitled to a dividend, so the delivery price must be discounted to reflect that futures holders aren't paid a dividend.
Fortunately, if all we care about is getting an implied interest rate closest to SOFR, the no-arbitrage arguments above still ensure that we're getting a pretty good one, just on a slightly different "asset". In particular, the first caveat implies the returns for a long future will depend on when the index rises and falls, being higher if it rises quickly at first and later flatlines than if it had grown uniformly. The second implies that our position is only exposed to capital appreciation of index constituents, not their dividends, though a dividend reduction is implicitly better for us but indifferent for holders of index constituents. Most of us are probably indifferent to the first caveat considering it makes a very small difference and doesn't imply any less diversification. For the second, one could argue that having dividend exposure is better-diversified because dividends aren't perfectly correlated with asset returns, but there's nothing mathematically canonical about a one to one ratio of dividend exposure to capital appreciation exposure, and those conducting this strategy in practice will likely end up with a mix of futures and ETFs anyway given that ETFs can be used as margin for futures. I'll probably do a CAPM analysis on this at some point because this has made me curious, but it could turn out that whatever ratio such investors end up with is actually better than one to one. Conversely, dividends, even qualified ones, are actually quite bad from a tax perspective5, though we'll see below that this doesn't matter much because futures in general are probably worse for long-term investors.
But let's say we're not satisfied with futures giving us slightly different exposure, or we really want to compare the implied rate of futures to that of other instruments (which we will attempt in the programming section below). The first issue is more or less impossible to hedge out. Institutions do it by trading "forward contracts" (which are over-the-counter futures contracts settled "the old way", all at once at expiration, rather than by marking to market), but retail investors can't access these, and as far as I'm aware there isn't even any public data on them. In principle, we could go to extreme lengths and e.g. calibrate some stochastic model to find the covariance between stocks and rates, which turns out to more or less encode the entire adjustment we'd need to make, but this would be empirical, not market-based. Luckily, the differences tend to be pretty small for short-dated contracts (which are usually all we should care about due to tax implications we'll explain below), so we can probably ignore this when computing rates at the cost of some precision.
On the other hand, dividend yields can be quite high, typically 1-2% on the S&P 500, so we really need some way to account for these. Fortunately, CME offers quarterly and annual dividend futures for a few indices, which pay out the sum of dividends in that quarter or year at the end of that quarter or year. Their quarterly futures are offered about a year out, and their annual ones to about 5 years out. The problem is, the sum of dividends over the period we hold the future isn't even the quantity we want to hedge: if we instead held all the SPX constituents, we would get not only the dividends, but the interest they generate between when they are paid and when we liquidate the position. That means the difference between the dividend futures and what we want to hedge is a quantity depending on both the future risk-free rate and the temporal distribution of when the dividends are actually paid. Luckily, this difference is also a pretty small quantity, and it can be reasonably approximated (for purposes of computing implied rates) by assuming the dividend is paid at the end of each quarter and invested at market-implied forward rates until the position is liquidated. But we'll unfortunately never be able to perfectly hedge the difference with market-traded instruments here, either.
Still, one can't deny the no-arbitrage arguments showing that futures offer close to risk-free rates, and in this sense, they blow broker margin out of the water. And it's true exchanges only offer them on a few indices and commodities rather than individual stocks, and that their exposure is to weird approximations of the investments we want rather than on the real thing, but many retail investors chiefly partake in set-it-and-forget-it index investing. For these investors, the variety is likely satisfactory, and they probably don't care that their investment won't perfectly track the index as long as it's close enough. Tragically, though, the other caveat is that they're taxed at Section 1256 rates, which means that capital gains on them are assessed at 60% of the taxpayer's long-term capital gains rate plus 40% of the short-term rate. This makes them great for speculative investors who are generally subject to the short-term rate, but unattractive to long-term retirement investors who usually pay the lower long-term rate, and this may even outweigh the margin savings for the latter group. If one's investment goals somehow escape this catch-22 (for example, if one holds all futures in a tax-advantaged retirement account), futures are indeed likely to be a good strategy, but retail investors with holdings in taxable accounts will probably need to look elsewhere.
Calls, puts, and synthetic futures
If you've ever read stories of retail investors using massive amounts of leverage and losing their entire investment, odds are these included options contracts, and you might be wondering if we can use them to lever up our positions at competitive rates. While they are indeed excellent sources of leverage, some nuances affect whether they can recreate the exact return profile of a loan as well as whether they use the same Section 1256 capital gains rates as futures. This section will explain the basics of options, then look at how we might use them to replicate the returns of futures contracts, as well as give motivation for the more generally-applicable strategy of box spreads discussed in the next section.
Options market crash course
There are two types of options, calls and puts. A call is a contract where the buyer has the right, but not the obligation, to buy a specified amount of an underlying asset at a specified price (the "strike price") from the seller any time before, in the case of American-style options, or on, in the case of European-style options, a specified future date (the "strike date"). Or at least, they used to all work like that – currently, the market has "cash-settled" options, which function similarly to futures in that they are guaranteed by clearing houses and accounts are marked to market at the end of the day, as well as "equity-settled" (in commodities, "physically-settled") options, which are still guaranteed by clearing houses and require collateral, but are not marked to market and require the underlying asset to actually change hands when a contract is exercised. Unlike futures contracts, the buyer of a call pays some amount of money to the seller to acquire the contract, called the "premium" (otherwise, recalling that the buyer has no obligation to exercise the contract, it would be impossible for the seller to make money). The returns for an equity/physically-settled European-style call, or an American-style call that is held until its expiration date, relative to the price of the underlying asset look like this for the buyer and seller:
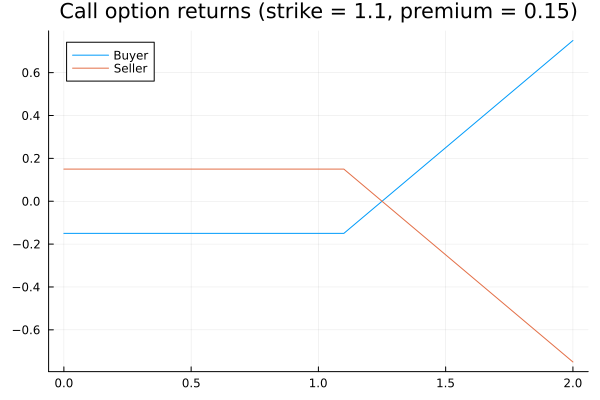
For the buyer, the returns to the left of the strike price are a flat loss because the buyer loses the premium (and the returns it could have generated at the risk-free rate) and cannot profit from exercising the call as he would end up buying the underlying asset for more than its market price; the return increases with the price of the stock to the right of the strike price because the buyer still loses the time-adjusted value of the premium, but is able to buy the security for the fixed strike price and sell it at the higher market price, pocketing the difference between the two. The seller's graph is essentially the opposite, always keeping the premium but being obligated to purchase the underlying asset at a higher-than-fair value if the market price ends up higher than the strike price, losing the difference. In general, call options are referred to as "in-the-money" when the market price exceeds the strike price (even when this doesn't make up for the premium), "at-the-money" when these are (roughly) the same, and "out-of-the-money" when the market price is below the strike price.
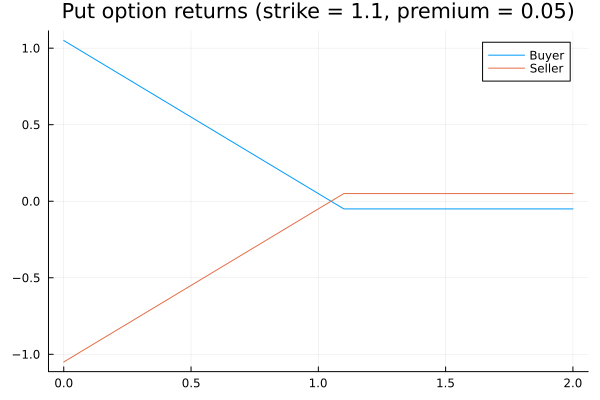
The other type of option, a put, is a contract where the buyer has the right, but not the obligation, to sell a specified amount of an underlying asset at a specified price (the "strike price") from the seller any time before, in the case of American-style options, or on, in the case of European-style options, a specified future date (the "strike date"). Similarly, the buyer pays a premium for the contract, but this time the buyer makes money when the market price is below the strike price at the time of expiry. The returns for an equity/physically-settled European-style put, or an American-style put that is held until its expiration date, relative to the price of the underlying asset look like this for the buyer and seller:
Synthetic futures
You might have noticed something from looking at those return graphs – if we add the graphs for the buyer of a call and the seller of a put (with the same strike price), we just end up with a diagonal line, something of the form \[V_1 = S_1 - K + (C^{(K)}_p - C^{(K)}_c)(1 + r),\] where \(S_1\) is the underlying asset price at expiration, \(K\) is the strike price, \(C^{(K)}_p\) is the put premium at strike \(K\), \(C^{(K)}_c\) is the call premium at strike \(K\), and \(r\) is the risk-free rate over the period. This means that if we buy a call and sell a put at the same strike price, and the put we sold isn't exercised early (in the case of American options), we're effectively paying \(S_0r\) (with \(S_0\) the initial stock price) in interest (debited/credited as \(C^{(K)}_p - C^{(K)}_c\) up front, then \(S_0(1 + r) - K\) at expiry) to borrow one unit of the underlying asset! Indeed, the same no-arbitrage argument from the futures section of this article also works here to show that \[(C^{(K)}_p - C^{(K)}_c)(1 + r) - K = -S_0(1 + r)\] (here \(S_0\) is the initial underlying asset price), as holding the underlying asset using borrowed money is again a replicating strategy6. Also, since the times at which interest is effectively debited and credited depend on the strike we choose, we can essentially give ourselves an implicit loan by choosing a very low strike (though we must be careful to choose a strike that is sufficiently liquid). Finally, if the underlying offers dividends, we do still have to adjust for these, but equity/physically-settled options don't require the same convexity adjustment as the futures did because they are not marked to market (for cash-settled marked-to-market options, roughly the same caveats apply).
We shouldn't get our hopes up yet, though; for those of us in Burgerland, most options are American-style, meaning they can't be used to make synthetic futures without the risk of somebody exercising the put early. Worse yet, all the European-style options offered by American exchanges I know of are only available on broad ETFs and commodities and are cash-settled (and thus also require convexity adjustments and have capital gains taxes falling under Section 1256, between the short and long term rates) – these have exactly the same drawbacks as the regular futures! This seems pretty bleak, but surely one could still benefit from long-term synthetic futures made from equity-settled options listed on European exchanges like Eurex, right? The answer is technically yes if you're willing to open an offshore brokerage account, but this comes with fees and hassle that probably don't make sense for retail. Why is this the case? This forum post seems to paint a pretty bleak picture of US regulation in the area, though it's from way back in 2007 and thus it's possible regulations have changed since then. Either way, I can't trade them in my Schwab account, so the effect is the same: it seems the only retail investors who can realistically use this strategy to escape a weird US tax law are non-Americans.
Box spreads
Despite synthetic futures turning out not to be useful in most cases, I promise there's a point to the last section other than a rant about outdated SEC policies. In particular, think about what would happen if we made a synthetic future – that's buying a call and selling a put – at one strike, say $20, and took the opposite position – selling a call and buying a put – at a different strike, say $10. The results would just cancel out and we'd be left with zero profit, right? Indeed, a quick graph confirms our suspicions:
Explicitly, the value of the position at expiration, if net premiums are invested/borrowed at the risk-free rate and in the notation of the last section, is \[S_1 - 20 + (C^{(\$20)}_p - C^{(\$20)}_c)(1 + r) - S_1 + 10 + (C_c^{(\$10)} - C_p^{(\$10)})(1 + r).\] As we saw before, \[(C^{(\$20)}_p - C^{(\$20)}_c)(1 + r) - 20 = S_0r = (C_c^{(\$10)} - C_p^{(\$10)})(1 + r) + 10\] (our calculation for the synthetic futures didn't depend on the strike), so the positions cancel out and the time-adjusted return is $0 regardless of what happens to the underlying – there's no free lunch, after all. But if we look at when the various payments happen, the premiums, \(C^{(\$20)}_p - C^{(\$20)}_c - C_c^{(\$10)} + C_p^{(\$10)}\), are credited to our account up front, and only at expiration is the differences between our strikes \(S_0(1 + r) - 20 - (S_0(1 + r) - 10) = -\$10\) debited7. It may not be immediately clear from the symbolic notation we used for the premiums, but rearranging the equation above, \[S_0(1 + r) - S_0(1 + r) = 0 = (C^{(\$20)}_p - C^{(\$20)}_c - C_c^{(\$10)} + C_p^{(\$10)})(1 + r) + \$10 - \$20,\] and thus we have used this spread to effectively borrow \(\$ 10(1 + r)^{-1}\) and repay \(\$ 10\) – that's the same as a loan!
Thus, we can use this strategy of a "box spread" – "buying" and "shorting" synthetic futures at different strikes – to effectively borrow (and lend) money using the options market, with our margin requirement enforced by the clearing house as our collateral and the clearing house serving as a guarantor to whomever takes the position as the lender. Better yet, we don't even have to make the box spread on the same security we want exposure to – any asset that the clearing house sees as satisfactory collateral is on the table, usually including equities, bonds, and other conventional instruments, meaning we're not restricted to just products with actively-traded options chains. In practice, this means most box spreads are traded on S&P 500 index options, which generally have the most volume and thus the smallest bid-ask spreads. Some options exchanges even allow "bundling" of the four "legs" of the box spread, where investors can offer bids and asks on the entire group of contracts, which must be bought all at once by another market party (who effectively uses them as an alternative to other secured lending markets, see the section below), often further reducing the impact of the bid-ask spread.
Do box spreads suffer from the same Section 1256 tax drawbacks for long-term investors? The answer is complicated: while all feasible options products that could be used to construct box spreads are cash-settled and thus subject to Section 1256, "interest" paid on box spreads is assessed as a capital loss in the tax code, which can be used (in the same year) to offset any kind of gains, whether short-term or long-term, provided gains in the same categories (in this case, 40% of the box spread losses are counted as short-term and 60% long term) have already been offset by losses in the same categories. For long-term investors, this is likely acceptable – not only can box spread "losses" offset their long-term gains, they can even offset some short-term gains. Compared to margin, when itemizing, the interest deductions can offset all net investment income, whether short-term or long term, effectively on a prorated basis, which might be better in some cases, but this isn't clear-cut and depends on the situation. There are also considerations that section 1256 losses can be carried to different tax years while interest deductions can't. The nuances of this can be complicated, but generally the tax implications of box spreads do not invalidate them for wide swaths of investors like the other two strategies do, and often they're actually better than margin with respect to taxes.
The repo market, SOFR, and how investment banks get leverage
It seems box spreads will be satisfactory for a large majority of retail investors, but all these roundabout strategies beg the question: why can't we just do whatever big institutions do to get secured credit? Actually, many of them just use margin; recalling that Interactive Brokers was willing to offer just a 52bp spread over SOFR on balances over $200,000,000 (chump change to many hedge funds, asset managers, etc), it's clear that big enough account sizes have much more negotiating power than retail, and thus can demand better rates. However, and in spite of the fact that margin lenders seem to have exceedingly favorable loan terms, a margin loan secured by a firm's assets is still not completely risk free, and thus will never be given at quite the "risk-free rate". Why? If a firm that has borrowed on margin declares bankruptcy, the lender cannot immediately seize its collateral to cover the loan; instead, these assets are frozen and the lender must go through lengthy bankruptcy proceedings just like any other creditor, and may not even recover the full amount.
To work around this possibility, lenders had to get creative. What if, instead of lending cash secured by collateral, lenders instead "bought" the collateral one day with the obligation to "sell" it back the next for a slightly higher price? Then if the firm they "bought" it from declared bankruptcy, the collateral would legally be the lender's whether or not the borrower were able to repurchase it. These repurchase agreements, or "repos" (presumably "repu" didn't sound cool enough) are the primary way that the largest banks and broker-dealers effectively "borrow" money. In practice, the collateral is almost always treasury bonds (but can be e.g. stocks or other liquid assets8) and there is usually a third party bank (almost always BNY Mellon) holding the collateral, to, among other reasons, protect the borrower in case the lender defaults on their obligation to buy (these are "tri-party repos"). We can now finally define SOFR: it is a rate published by the Federal Reserve each night to reflect the "average" overnight rate attached to these repurchase agreements. In fact, the Federal Reserve is often a party to this market to help implement its monetary policy, borrowing or lending to move rates up or down respectively.
Why can't retail investors access this market? Actually, they effectively can if they only want to lend; commercial banks with money market accounts are some of the largest lenders in the repo market, are FDIC insured, and in many cases return rates at or even above SOFR9. But to be on the receiving end, prospective borrowers must generally cultivate relationships with individual lending institutions as trading is over-the-counter, and the only institutional borrowers which tend to do so are the largest of the large; according to BNY Mellon data, it only had 118 total accounts belonging to borrowers for purposes of repurchase agreements (though it's possible that broker-dealers participate on behalf of, or to provide margin to, their customers). So it looks like retail will have to make do with futures and box spreads.
Comparison of implied rates
How to Compare Fixed and Floating Rates
Now that we understand how all these methods give implied leverage, we can compute the implied rates and compare them to SOFR. There's just one issue: SOFR (and broker margin) operate with floating overnight rates, while derivatives contracts effectively (roughly, if marked-to-market) give a fixed interest rate until expiry. The usual way to account for this is by looking at overnight index swap (OIS) rates over the same time period. Overnight index swaps are contracts where one party agrees to pay a second party a fixed interest rate in exchange for the second party paying the first a floating rate (now usually SOFR or the federal funds rate) over a specified period – clearly the market fixed rate among these contracts represents the market "fixed risk-free rate" over the specified period. However, I can't find free OIS data anywhere on the internet with enough granularity to be useful any time except a handful of dates – in particular, we'd need data for swaps expiring on the same day as futures and options contracts, but the only source I can find only has granularities of 1 month, 2 months, 3 months, 6 months, and then into years. This makes it seem that we can only compare implied rates apples-to-apples at around four dates per expiry, some of which overlap as longer-term derivatives are only offered at 3-month intervals (there are other expirations, but they're only tradable a few weeks in advance).
Luckily, there's another approach, though it might be a bit less precise: SOFR futures. These operate like other cash-settled futures described above, but instead of being based on the price of an index or commodity, their price is determined by SOFR compounded over a three-month period10. Specifically, at expiration, the contract value (the "points" it trades at, before the contract multiplier) of a SOFR future with a particular reference month is \$100 divided the geometric mean of annualized (compounded) SOFR over the three month period starting on the third Wednesday of the reference month and ending on the third Tuesday of the third following month, inclusive. For instance, the September 2024 SOFR future expires with contract value equal to \$100 over the geometric mean of annualized compounded SOFR from September 20 to December 24. Unfortunately, quarterly expirations for most other futures are on Fridays, not Tuesdays, so there is in practice a 3-day gap, but if we consider the actual differences involved – even a 500 bp difference on both the non-matching Wednesday, Thursday, and Friday would only result in a \(1 - (1.05)^{\frac{3}{90}} \approx 16.2 \text{bp} \) difference over the course of a (~90 day) quarter – this probably doesn't matter that much. We will use this approach below.
Implementation and results
Now, we'll actually download futures and options data and plot the implied rates of each approach at different dates, all assuming we want to borrow until December 2025. Specifically, we'll always use one unit of the 5000-6000 box spread on SPX index options (a ~\$100k loan due to the contract multiplier of 100, though it is the repayment amount and not the borrowed amount which is fixed at \$100k) for simplicity. We also won't use synthetic longs as these are generally worse than futures (on SPX at least), both from a quality-of-data perspective and an implied rate perspective, due to the bid-ask spread (and both are cash settled so are the same for tax purposes, as mentioned above).
Here's the code block where we set up imports and get data from Yahoo finance.
using YFinance, CSV, DataFrames, Dates, Plots;
startd=Date(2024, 10, 14)
futstartd=Date(2024, 10, 14)
boxstartd = Date(2024, 1, 1)
endd=Date(2024, 10, 20)
#Get OLHC data needed for computing implied rates for futures and box spreads
#SPX spot and futures
SPXspot = get_prices("^SPX"; interval="1d", startdt=startd, enddt=endd) |> DataFrame;
SPX25 = get_prices("ESZ25.CME"; interval="1d", startdt=startd, enddt=endd) |> DataFrame;
#SDA futures (futures on SPX's dividend index; see relevant section on futures and dividends)
SDA24 = get_prices("SDAZ24.CME"; interval="1d", startdt=startd, enddt=endd) |> DataFrame;
SDA25 = get_prices("SDAZ25.CME"; interval="1d", startdt=startd, enddt=endd) |> DataFrame;
#SPX total return at start of year and now (to compute dividends already paid this year)
VOO = get_prices("VOO"; interval="1d", startdt=startd, enddt=endd) |> DataFrame;
VOOdivd = get_dividends("VOO"; startdt=Date(2024, 1, 1), enddt=endd) |> DataFrame;
#SPX options (call/put at 5000/6000)
C5000 = get_prices("SPX251219C05000000"; interval="1d", startdt=boxstartd, enddt=endd) |> DataFrame;
C6000 = get_prices("SPX251219C06000000"; interval="1d", startdt=boxstartd, enddt=endd) |> DataFrame;
P5000 = get_prices("SPX251219P05000000"; interval="1d", startdt=boxstartd, enddt=endd) |> DataFrame;
P6000 = get_prices("SPX251219P06000000"; interval="1d", startdt=boxstartd, enddt=endd) |> DataFrame;
#Get OLHC for Sep 24, Dec 24, Mar 25, Jun 25, Sep 25, Dec 25 SOFR futures
SOFRSep24 = get_prices("SR3U24.CME"; range="5d", interval="1m") |> DataFrame;
SOFRDec24 = get_prices("SR3Z24.CME"; range="5d", interval="1m") |> DataFrame;
SOFRMar25 = get_prices("SR3H25.CME"; range="5d", interval="1m") |> DataFrame;
SOFRJun25 = get_prices("SR3M25.CME"; range="5d", interval="1m") |> DataFrame;
SOFRSep25 = get_prices("SR3U25.CME"; range="5d", interval="1m") |> DataFrame;
I originally wanted to compute implied rates for each strategy over a long period, e.g. since the start of the year, which could give us interesting information about how the spreads vary during e.g. different macroeconomic conditions. However, Yahoo finance doesn't have historical data for already-expired SOFR futures, and doesn't seem to keep historical (but unexpired) SOFR future data longer than 5 days! So while this code is written very generally, I unfortunately can only show fixed rates implied by SOFR futures and the SPX futures strategy (the latter because fixed SOFR is needed to properly determine implied dividends) from October 3-8, 2024 here.
Also, our SPX-futures-implied rates are not free of issues. Recalling from the theory section that (a) the quarterly dividend index isn't a perfect dividend hedge and (b) stock index futures exhibit convexity, this was bound to happen to some extent, but it's actually made much worse by the fact that we can't get historical quarterly dividend futures data from Yahoo at all. It does have pages for these contracts, and we can get current price quotes, but e.g. the page for the December 2025 contract only has data for one day in October at the time of writing. I suspect Yahoo Finance operates by lazily looking up exchange data for a contract only when somebody actually navigates to the corresponding page, then storing it permanently, and I'm just the first person to use Yahoo's data for obscure derivatives contracts like this.
Finally, it looks like Yahoo doesn't have historical bid-ask data for the options, only open, high, low, and close. So while there's technically enough data to compute box spread rates from these out to several years, none of it is very good because these options aren't so liquid that the first and last trades of the day happened at the same time for every option we're looking at. We'll still go ahead and write up code that will produce a chart comparing implied rates for illustrative purposes, but note that the computed box spread yields will jump around a lot and should probably be taken with a grain of salt.
#Get SOFR data into workable form
function byday(sofrdf)
cleaned = sofrdf[.!isnan.(sofrdf.open), All()]
withday = transform(cleaned[Time.(cleaned.timestamp) .>= Time("13:30") .&& Time.(cleaned.timestamp) .<= Time("20:00"), :], :timestamp => (x -> Date.(x)) => :day)
grouped = groupby(withday, :day)
return combine(grouped,
[:open, :timestamp] => ((x, y) -> x[argmin(y)]) => :open,
:low => minimum => :low,
:high => maximum => :high,
[:close, :timestamp] => ((x, y) -> x[argmax(y)]) => :close
)
end
SOFRthisperiod = byday(SOFRSep24)
daysLeftThisPeriod = Dates.value.(Date(2024, 12, 24) .- SOFRthisperiod.day)
SOFRfutureperiods = [byday(SOFRDec24), byday(SOFRMar25), byday(SOFRJun25), byday(SOFRSep25)]
#The St. Louis Fed's published SOFR index
#Dividing an earlier date by a later one gives the discount factor (and vice versa)
SOFRIdx = DataFrame(CSV.File("SOFRINDEX.csv"))
lastweekday(day::Date) = dayofweek(day) < 6 ? day : (dayofweek(day) < 7 ? day - Day(1) : day - Day(2))
discount(from::Date, to::Date) = parse(Float64, SOFRIdx[SOFRIdx[:, "DATE"] .== lastweekday(from), "SOFRINDEX"][1]) / parse(Float64, SOFRIdx[SOFRIdx[:, "DATE"] .== lastweekday(to), "SOFRINDEX"][1])
sofrsincestartofquarter = ((100 ./ SOFRthisperiod.open).^(1/4) .* parse.(Float64, SOFRIdx[SOFRIdx[:, "DATE"] .== Date(2024, 9, 20), "SOFRINDEX"]) ./ parse.(Float64, subset(SOFRIdx, :DATE => (x -> vec(reduce(|, reduce(hcat, [d .== x for d=SOFRthisperiod.day]); dims=2)))).SOFRINDEX))
#Compute fixed rate implied by SOFR
SOFRImpliedRate = (sofrsincestartofquarter .* (prod(100 ./ transpose(reduce(hcat, [getindex.(SOFRfutureperiods, i, "open") for i=1:4])), dims=2)).^(1/4)).^(365 ./(365 .+ daysLeftThisPeriod))
dates = collect(startd:endd-Day(1))[dayofweek.(collect(startd:endd-Day(1))) .< 6]
gooddates(df) = df[[Date(df.timestamp[i]) in dates for i in 1:size(df)[1]], :]
plot(dates, SOFRImpliedRate; labels="SOFR futures")
daysuntilD25 = Dates.value.(Date(2025, 12, 19) - dates)
#Implied SOFR-appreciated cost of carry, not including interest (so negative due to dividends), for SPX
#Assumes remaining dividends (beyond what VOO distributed) in the current year are paid uniformly over remainder of year
impliedremainingdiv = (Dates.value.(Date(2024, 12, 24) .- dates)/92).*
(gooddates(SDA24).open - sum((SPXspot.close[end]/VOO.close[end]).*VOOdivd.div)./sofrsincestartofquarter).*sofrsincestartofquarter
impliedfuturesrate = ((gooddates(SPX25).open .+ (impliedremainingdiv .+ gooddates(SDA25).open).*(prod(100 ./transpose(reduce(hcat, [getindex.(SOFRfutureperiods, i, "open") for i=1:4])), dims=2)).^(1/4))./gooddates(SPXspot).open).^(365 ./daysuntilD25)
plot!(dates, impliedfuturesrate; labels="SPX futures")
impliedboxspreadrate = (1000 ./(gooddates(P6000).open - gooddates(C6000).open + gooddates(C5000).open - gooddates(P5000).open)).^(365 ./daysuntilD25)
plot!(Date.(gooddates(P6000).timestamp), impliedboxspreadrate; labels="Box spreads")
savefig("../images/interest-rates/computedrates.png")
return nothing
And here is the graph showing the rates we computed:
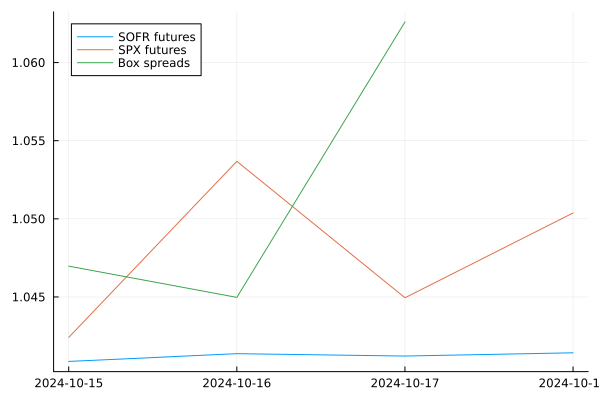
Note: Yahoo finance has a gap in its data for the call at strike 5000 on the 18th.
Clearly, the implied term SOFR and futures-implied rates over time don't really tell us much given the span of 3 days, and the box spreads are all over the place due to reasons mentioned above, but the code should at least be a reasonable illustration of how one would go about implementing this assuming the data were better. If you're actually curious about "real" box spread rates (e.g., if you actually want to use them instead of just studying them), I'd recommend boxtrades.com (specifically, this is their version of what we were trying to compute), which uses data from "bundled" box spreads – i.e. complex orders allowed by some exchanges where all four "legs" of the box spread must be filled at once by the same party – to build its curve (Yahoo finance obviously has nothing like this for us to use). If you're wondering whether using box spreads in real life can really overcome the bid-ask spread and liquidity issues, SyntheticFi, the startup whose data boxtrades.com uses, claims it can offer its clients SOFR+40bp simply by placing box trades on their behalf, presumably including a spread for itself, which is fairly competitive (even Interactive Brokers has a 10bp higher spread on their top bracket, balances of over \$200 million or more).
Conclusion
Clearly, retail investors can do much better than broker margin when accessing leverage, and the conclusion we can draw from the theory section is that generally speaking, box spreads are the best way to do this. In practice, a retail trader could likely get away with reading the few sentences describing the implementation of a short box spread and simply construct one without any knowledge of the rest of this article, but I hope that this article has provided both a theoretical motivation for how one would discover this type of leverage and satisfactory theoretical arguments showing that rates must be good.
Footnotes:
Also, I find traditional means of reporting bond yields to be pointless and anachronistic. Most unsophisticated investors who invest directly in bonds these days are exclusively buying treasuries, which have essentially negligible credit risk, and increasingly use diversified bond ETFs to gain exposure to e.g. corporate or foreign government bonds; for these investors, the lack of comparability between APYs of bond ETFs and obtuse semi-annual par yield calculations would only serve to confuse. At the other end, sophisticated (in the usual sense, not the regulatory one) investors buying bonds from individual issuers should have no trouble nowadays writing computer programs which account for time value and credit risk on each individual coupon payment, so the method the issuer uses when advertising a yield value should matter little to these investors anyway
Usually, futures (and options, which we will see later) have a "multiplier", so that even if a future quote is e.g. 120 points, that might correspond to a notional value of \$12,000 (in other words, if the future's value suddenly went to 0, a seller/short position holder who bought in at 120 points would see a \$12,000 profit).
This type of contract still exists, and is usually referred to as a forward contract, but these generally trade over the counter rather than on exchanges.
We speak with respect to a (the) risk-neutral measure. However, even in the constant-rate case, marking-to-market may introduce path dependence into an investor's subjective valuation based on their beliefs about the true probability measure, as this need not be true for all possible probability measures.
This is because they essentially force one to pay capital gains every year, whereas pure capital appreciation only triggers a capital gain when the asset is sold. This is not just bad in some far-off estate planning step up in basis sense, but is also bad for those who plan to spend the entirety of their portfolio. Indeed, if one pays capital gains taxes after one year, one can no longer invest the sum paid, but if one only pays capital gains taxes in one's second year, the sum that would have been paid in the first year remained implicitly invested in the second year, and the investor can pocket the interest it generates (after paying taxes on that interest), even if the investor still has to pay the entire "principal" (with respect to the first year) in capital gains taxes in the second year.
This should also make sense intuitively because no matter what, when buying a call and selling a put, the investor ends up buying the asset at the strike and selling it at market price. If the call expires in the money, the investor exercises it at expiration to buy the asset, then sells it at market prices. If the put expires in the money, the other party exercises it at expiration to sell the asset to the investor at the strike, who then has to sell it at market prices.
If the options are marked to market instead of physically-settled, the loan is effectively paid back over the life of the transaction, though the amount paid back remains a constant amount once properly discounted.
Fun fact: mortgage-backed securities are also allowed as collateral in this market. In the leadup to the 2008 financial crisis, this allowed firms like Lehman Brothers to become very exposed to them, as it could leverage its mortgage-backed securities in the repo market to buy and securitize more mortgages. Then, once repo market lenders began to distrust mortgage-backed securities as collateral and liquidity dried up, Lehman Brothers had to sell some, thereby lowering the value of the rest of the mortgage-backed securities it owned and used as repo collateral, causing it to spiral into bankruptcy.
There are two ways they can do this. One, they hold riskier or unsecured instruments, often investment-grade short-term corporate bonds (the FDIC still insures them though). Two, they can offer high rates for some period as a promotion, then lower them and hope you won't notice, hope you use e.g. their checking accounts with bad interest, or make their money back in fees. As of right now, I couldn't find any exceeding SOFR, probably because it increased a bit since the beginning of the month, but I see one at 5.3% APY which is only 18bp off. Another alternative is government-focused money market funds, which are not FDIC insured but in practice are essentially risk-free as they only lend via the repo market or buy short-term treasuries.
They also offer 1-month SOFR futures, but these track the arithmetic mean instead of the geometric mean for some reason, meaning they don't actually exactly correspond the market's expected returns of money invested at SOFR over the relevant period.