The "Arbitrage-Free" Price of a Roth IRA
An introduction to financial mathematics through the lens of personal finance
Table of Contents
As a college student, when I accepted an internship opportunity last summer, it seemed like the perfect opportunity to invest in Roth retirement accounts. For those unfamiliar with Roth accounts or the US tax code in general, a Roth is a tax-advantaged retirement account contributed to with money on which income tax has already been paid, such that holdings in the account are not subject to capital gains taxes (read e.g. this for more detail). I won't get into the weeds comparing Roth accounts to other retirement accounts, but my predicted future gross income made Roth the clear choice.
But how much will the Roth save me over a taxable account? Googling this question produces a plethora of sites like this one or this one calculating this number, but every one I've seen so far has been wrong (or to be generous, answered the wrong question). Let's investigate the error and try to come up with our own valuation based on the price of a "replicating strategy" for Roth assets using normal taxable ones, motivating the ideas of no-arbitrage pricing and leverage-enhanced portfolios along the way. We'll even use what we find to make a calculator of our own. Finally, we'll look at what our findings mean in the context of US tax policy, and observe how a misleading intuition about the phrase "savings over a taxable account" also contributes to an irrational bias that has caused even relatively-savvy investors to undershoot their own risk tolerances for decades.
The critical mistake
Both of the calculators I linked calculate the tax savings of a Roth account by simply determining what the price of the portfolio given by a certain investment structure – say investing a fixed amount of money per year at a fixed percent annual return – will be at some target retirement date, and then multiplying by a ~15-20% long-term capital gains rate. In fact, this correctly approximates the amount of money not paid to the IRS that otherwise would have been if one held the exact same portfolio in a taxable account. To visualize this, we plot the tax-adjusted return vs. pre-tax return of the same portfolio in taxable or Roth (this is trivial) assets, noting that, since capital losses carry over indefinitely, we model tax-adjusted losses in the taxable portfolio as reduced by the marginal capital gains rate:
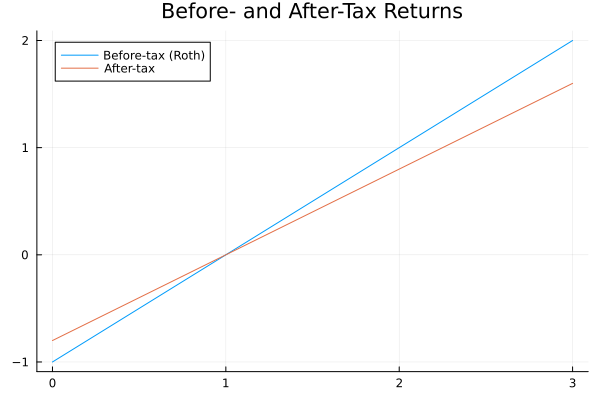
So why isn't the above calculation the right way to value the Roth? Certainly the Roth is worth more than the taxable assets if the value of the portfolio goes up, but if the value goes down, it actually becomes less valuable, since we can't write off any losses in a Roth. That means, counterintuitively, that the Roth is riskier than the taxable account when both are invested in the same portfolio. If it helps, I'll illustrate with two examples:
Let \(x\) be the pre-tax rate of return on some financial instrument/portfolio, and \(c\) be the marginal tax rate. Then the tax-adjusted rate of return is \(x(1 - c)\) in a taxable account, but is simply \(x\) in a Roth. That is, if we buy \(\$100\) of the portfolio and sell it for \(\$120\), \(x\) is \(1 - \frac{120}{100} = 0.2 = 20\%\), and if this happened in a taxable account with a marginal tax rate of \(20\%\), our tax-adjusted rate of return would be \(0.2 \cdot (1 - 0.2) = 0.16\% = 0.16\), for an after-tax profit of \(\$ 100 \cdot 0.16 = \$16\); if we had instead bought \(\$100\) of the portfolio in a Roth and sold at the same time, the tax-adjusted rate of return would equal the pre-tax return, so tax-adjusted gain would be \(\$100 \cdot 0.2 = \$20\), which is \(\frac{20}{16} - 1 = \frac{1}{1 - c} = 25\%\) better than the taxable account! On the other hand, if we had bought \(\$100\) of the portfolio and sold it for \(\$80\) in the taxable account, this would allow us to write off \(\$20\) worth of (possibly future) capital gains, which we'll model at the same marginal tax rate of \(\$20%\), turning our \(\$20\) pre-tax loss into a \(\$20 - \$20 \cdot 0.2 = \$20 (1 - 0.2) = \$16\) tax-adjusted loss, meaning we would have lost \(\frac{\$20}{\$16} - 1 = 25 \%\) more if we lost the same \(\$20\) in a Roth.
Of course, we've glossed over a few things with this model. For one, any writeoffs for capital losses are limited to one's capital gains in any particular year plus $3000, though they may be carried forward indefinitely – this means we may end up losing the time value of some of these losses until we can use them as writeoffs, or all the remaining amount if we happen to die early. However, long-term capital losses can also be used to offset short-term capital gains in the same tax year, which are taxed at a higher rate. For simplicity, and as is often the case in real life, we'll model it as a wash. Then our graph and calculations above are roughly accurate, and Roth accounts are indeed riskier than taxable ones. We often hear that investments should be evaluated on the basis of risk-adjusted returns1, so it makes sense that this increased risk would lower our valuation (i.e. how much we'd be willing to pay to invest in the Roth), but how can we account for this in a rigorous mathematical way2?
The power of leverage
It's clear from the graph that with the assumption about capital losses, Roth assets' return profile is the same as the profile for taxable assets, just scaled up by the marginal tax rate. In fact, if borrowing money were free, I claim we could simply borrow enough money to exactly replicate the tax-adjusted return of the Roth assets in a taxable account. This immediately follows because in this case, whether we started with money or borrowed it doesn't affect our returns from investing it. I won't go into detail as this is a special case of a later calculation, but we end up needing to borrow \(\frac{c}{1 - c}\) times our starting balance, where \(c\) is the marginal capital gains rate.
Of course, borrowing money can actually be quite expensive, as one look at the margin rates from any retail broker will demonstrate. But even when borrowing isn't free, we can still try to replicate the returns of the Roth by borrowing and investing as much money as we would if it were free. Then our returns would still be equal to those of the Roth, and our costs will only increase by the interest required to borrow enough money for the strategy. Assuming our portfolio is interest-rate-neutral, that cost doesn't even depend on the underlying asset returns! Thus, it seems like the Roth is "worth" this cost of borrowing. Let's explore how we can formalize this concept mathematically.
The notion of an arbitrage
Suppose we lived in a world where "Roth assets" were tradable on typical markets (alongside, and just like, their taxable counterparts). Then we should certainly expect they would be offered at a price where there's no strategy trading in "Roth" and/or "normal" assets with starting value equal to 0 (i.e. the only investments can come from borrowed money, shorted stock, etc) that never lose money and make money at least some of the time, otherwise savvy investment bankers would execute them in so much volume that prices would move and the strategies wouldn't profitable anymore.
This is an informal statement of the no-arbitrage principle, which is the idea that "perfect" markets should not permit strategies yielding guaranteed gains with no net initial investment, or arbitrages. Continuing our example, suppose now that we're an investment banker trying to make money in this hypothetical situation – crucially, we can both borrow and lend (with no risk of default) money at some interest rate \(r\), called the risk-free rate (this is needed for a unique arbitrage-free price – the results when we borrow and lend at different rates are out of scope here). Call the price of some tradable asset \(S_0\) now and call \(S_1\) (a random variable, though we won't formalize what this means in this article) its tax-adjusted price at some target date ("time 1"). We'll model trading strategies as triples \(\phi = (\alpha, \beta, \gamma)\) where \(\alpha\) is the number of taxable units of a risky asset \(S\) to hold (if negative, to short)), \(\beta\) is the money to lend (if negative, to borrow) at interest rate \(r\), and \(\gamma\) is the number of Roth units to hold (if negative, to short), with some initial price \(R_0\) and price at time one of \(R_1 = S_0 + \frac{S_1 - S_0}{1 - c}\) (where \(c\) again models the marginal capital gains rate). The value of a strategy \(\phi = (\alpha, \beta, \gamma)\) at time \(1\) is thus \(v_1 (\phi) := \alpha S_1 + \beta (1 + r) + \gamma R_1\). Then an arbitrage is a strategy \(\phi\) with \(v_0 (\phi) = 0\), \(v_1 (\phi) \geq 0\) a.s., and \(P(v_1(\phi) > 0) > 0\).
The arbitrage-free price of a Roth
With the above notation, we claim that there is a unique arbitrage-free price for \(R_0\) – that is, that there is only one possible \(R_0\) for which there does not exist an arbitrage opportunity in this market. As hinted at above, a good way to prove this is to find a trading strategy \(\phi\) that does not use \(R\) but exactly replicates the returns of \(R\) (so \(v_1(\phi) = R_1\) a.s.) – this is known as a replicating strategy for \(R\). If we had such a \(\phi\), then if \(R_0 > v_0(\phi)\), we could create a new trading strategy \(\psi\) by executing one "unit" of \(\phi\) and shorting one unit of \(R\) at time 0 (so \(\alpha_\psi = \alpha_\phi\), \(\beta_\psi = \beta_\phi\), \(\gamma_\psi = -1\)), loan out the rest at the risk-free rate, and we'll be left with \((R_0 - v_0(\phi))(1 + r) + v_1(\phi) - R_1\) at time 1. The last two terms cancel as \(v_1(\phi) = R_1\) a.s., so this is strictly positive almost-surely. Similarly, if \(R_0 < v_0(\phi)\), we could execute the "opposite" of \(\phi\) (i.e., take \(\alpha_\psi = -\alpha_\phi\), \(\beta_\psi = -\beta_\phi\)) and buy one unit of \(R\) (so \(\gamma_\psi = 1\)), loan out the remainder, and be left with \((v_0(\phi) - R_0)(1 + r) + R_1 - v_1(\phi)\), where again the last two terms cancel and the result is strictly positive. So if such a strategy \(\phi\) exists, we've ruled out all possibilities for an arbitrage-free price other than \(R_0 = v_0(\phi)\). Showing that a market where \(R_0 = v_0(\phi)\) is arbitrage-free is a little more complicated, and we'll do that after we find \(\phi\) itself.
To actually find a replicating strategy \(\phi\), we'll use the idea above of borrowing just enough money to invest in \(S\) that we replicate the returns of \(R\). Here \(R_1\) depends on \(S_1\) in a nice way, so it's not too hard to solve for possible α and β. Rewriting \(\alpha S_1 + \beta(1 + r) = S_0 + \frac{S_1 - S_0}{1 - c} = \frac{1}{1 - c}S_1 - \frac{c}{1 - c}S_0\) and noting that the first and second terms on the LHS and RHS depend on \(S_1\) and are deterministic respectively, it's clear that we should have \(\alpha = \frac{1}{1 - c}\) and \(\beta = - \frac{cS_0}{(1 - c)(1 + r)}\) to make the first and second terms equal respectively. So \(R_0 = v_0(\phi) = \frac{1}{1 - c}S_0 - \frac{cS_0}{(1 - c)(1 + r)}\). Note that if \(r\) is 0, this is exactly the strategy we found above when borrowing money is free.
We glossed over a very important detail above, which is that if \(R_0 = v_0(\phi) = \frac{1}{1 - c}S_0 - \frac{cS_0}{(1 - c)(1 + r)}\), then there are no arbitrages. This statement should seem suspicious – that quantity doesn't even depend on the distribution of \(S_1\)! To show there is no arbitrage, we must recall that this is the price of a replicating strategy for \(R\) in \(S\) and lending/borrowing. Thus, with \(R_0\) at this price, any \(\psi = (\alpha_\psi, \beta_\psi, \gamma_\psi)\) has the exact same returns as \(\psi' = (\alpha_\psi + \alpha_\phi\gamma_\psi, \beta_\psi + \beta_\phi\gamma_\psi\) (at both time 0 and time 1), where φ is the replicating strategy, so there is an arbitrage in our market with \(R\), \(S\), and borrowing/lending if and only if there is an arbitrage in a market with only \(S\) and borrowing/lending. This is only true in markets where the returns of the stock are strictly better or strictly worse than that of lending – i.e., a world where stocks either never go down or never go up as compared to the risk-free rate – which is obviously unrealistic (if this ever happened, investors would quickly borrow money to buy stocks or short stocks to lend money respectively until prices were "realistic" again – this is the no-arbitrage principle in action). This completes the proof for the particular case of a Roth IRA, and this idea can easily be extrapolated to prove one direction of the first fundamental theorem of asset pricing, an important theorem in financial mathematics, for our 2-period market model.
Toward a dollar value, and economic/budgetary considerations
Hopefully you're convinced that the price you would pay to invest in a Roth over a taxable account is \(\frac{1}{1 - c}S_0 - \frac{cS_0}{(1 - c)(1 + r)} - S_0\), where \(S_0\) is the sticker price of the assets you'll invest in right as you buy in and \(r\) is your interest rate over the entire holding period. We're almost done, but we have left one question unanswered: what is \(r\)? We alluded to this above, but the margin rates offered by retail brokers are at minimum multiple percentage points higher than what we can reasonably expect to lend at, threatening to contradict our assumptions used when calculating the arbitrage-free price. Luckily, even lowly retail traders can access institutional-quality implied interest rates using various derivatives strategies such as box spreads, which I discuss in a companion article here – in addition to discussing vital tools to access reasonably-priced leverage, this article also contains applications of our new arbitrage-free pricing idea, so I strongly suggest you read it. Both historically-speaking and looking at long-term box spread "yields" (as we do in that article), an APY of about 4% is attainable long-term (so \(r \approx (1.04)^t\), with \(t\) the holding period in years) – note that the bid-ask spread on the options comprising a box spread can in practice result in differences between implied borrowing and lending rates of a few tenths of a percent if we know we'll always be liquidity-taking, but we won't include that in our model.
At this point, the only thing that remains is to add our own calculator to let you find the real, inflation-adjusted value of a Roth for your personal circumstances. Note: for this calculator, we write "excess value" to mean the fair value of the opportunity to invest the specified amount of money in a Roth (which is equal to the difference in returns between the Roth and the replicating taxable strategy). "Inflation-adjusted" means discounted by the inflation rate, and "present value" means discounted by the risk-free rate (i.e., it's the amount we would pay right now for the opportunity to invest the money at whatever time in the future). Discounting is with respect to the time at which the money is invested in the Roth (our formula for valuing the Roth already discounts for the period that the money is invested at the risk-free rate).
Amount to invest each year (the calculator will automatically increase this with inflation). The statutory maximum for Roth IRAs is $7000, but conversion strategies or Roth 401(k)s can be used to exceed this in some cases: $
Current age:
Interest rate: %
Inflation rate: %
Capital gains (effective): %
Based on these numbers, the following graph shows the total inflation-adjusted excess value, as well as the present value (discounting at the inflation-adjusted risk-free rate), if the entire account is instantly liquidated at various retirement ages:
If the entire Roth is to be liquidated at age , this chart shows the inflation-adjusted excess value each year:
To simulate a more realistic retirement, let's suppose that instead of liquidating all at the same time, % is withdrawn each year (varying from year to year depending on total portfolio value, otherwise the calculation would depend on the rate of return and volatility) and the investor dies at age . In this model, check this box to model the value to both the investor and any heirs, who hold and eventually liquidate the entire (no withdrawals during this period) account years after the investor's death (10 is the longest they can hold it by law); otherwise, we'll model any funds the investor dies with as lost. Then the graph showing excess value vs target retirement date becomes
And with target age (same death/heirs settings), this chart shows the inflation-adjusted excess value from each year's contributions of the specified amount (as earlier contributions are held for longer):
Some notes on these charts:
- These obviously only model some very specific and contrived situations, mainly for the sake of being possible to calculate without assuming rates of return and volatility, as this article would quickly become a portfolio optimization seminar otherwise. The "realistic" retirement scenario will likely be in the right ballpark, but most real retirees have some money in Roth accounts, some money in traditional retirement accounts, and some money in taxable accounts, and optimize which they withdraw from based on tax bracket and required minimum distribution considerations – simulating these is out of scope for this article.
- If you know you won't access the money until retirement age, a Roth is (obviously) strictly better than a taxable account, so there's no actual point in trying to calculate this value for your specific scenario other than out of curiosity, which hopefully these calculators should appease. Feel free to try for your own personal scenario, although if you want to withdraw a fixed amount per year in retirement (like most real retirees), you'll also have to adjust for rate of return, volatility/sequence of returns risk, etc, which can get complicated.
- Neither chart gives nominal values because I don't think there's any point in knowing them. The second and fourth charts don't give present values because their main purpose is to show the value of the contributions to you in the years that you make them; the amount you would pay right now for the ability to invest an inflation-adjusted amount of money in a Roth IRA in exactly \(n\) years does not seem nearly as important to me as what that money would be worth right as you're investing it, and I didn't want to clutter the chart. If you really want to know this, though, the entire implementation of the calculator is in a script tag that you can modify with inspect element, and all you'd have to do is replace
inflwithratein a few places. - The minimum age to withdraw "interest" (realized gains) from a Roth IRA is 59½. I didn't enforce this as the minimum age with input validation because it's possible to retire for e.g. 1-2 years while living on "principal" only (e.g., withdrawing less than the amount you put in over your lifetime), but very early retirement dates in this scenario are likely impossible.
US budgetary considerations
Perhaps the one scenario where knowing a value like this is useful is calculating the total benefit of the Roth IRA across all US citizens. Surprisingly, it's hard to google what the average Roth IRA balance is – data is usually grouped into IRA vs 401(k), which doesn't matter because there are both traditional and Roth IRAs – but I'll try to reconstruct estimates as best I can. A 2023 Fidelity press release states that 61.2% of its customers' IRA contributions (in dollars) are to Roth IRAs. The 2021 census Survey of Income and Program Participation report indicates that 18.2% of the working-age population had some IRA account in 2020, that 81.1% of IRA owners contributed to their IRA, and that the median total annual IRA (across both Roth and Traditional) contributions among owners who contributed was $2514. Thus, assuming that the median total annual IRA contribution is close to the median, that Fidelity's customers are representative of the whole country in terms of proportion of traditional vs Roth contributions, that trends since 2020 roughly continue, and that Fidelity isn't doing weird things like double-counting contributions to traditional IRAs when they're converted to Roth, the total Roth IRA contributions in 2024 will be approximately \(2514 \cdot 0.182 \cdot 0.811 \cdot 0.612 \cdot 334,914,895 \cdot (1 - 0.222) = 64.3\) billion dollars (where the last two factors represent the current over-18 population, taken from Wikipedia, which cites the Census Bureau). This isn't quite enough to compute the excess value – we'd still need to know the dollar-weighted average time before withdrawal of this money – so let's throw out a ballpark estimate that the average dollar in a Roth IRA will spend 40 years there before the portion of the account it represents is withdrawn. Then at a 4% risk-free rate, and a 15% long-term capital gains rate, all reasonable assumptions for the average taxpayer, this year's contributions result in just a \(\frac{1}{1 - 0.15} \cdot 64.3 - \frac{0.15 \cdot 64.3}{(1 - 0.15)(1 + 0.04)^{40}} - 64.3 = 8.98\) billion dollar benefit (present value) across the entire country.
To put it bluntly, $8.98 billion is peanuts – if distributed evenly across the entire US population, this sum would be the equivalent of a $30 per person check. But a curious fact is that this is not the total loss in tax revenue to the IRS resulting from this policy. Indeed, suppose the average Roth portfolio generates a 10% nominal pre-tax return (which is to say, 6% over the risk-free rate) per year. If the expected 64.3 billion in contributions were instead invested in taxable accounts, with an additional \(\frac{1}{1 - 0.15}\) borrowed and invested, these contributions would generate a present value of \((64.3 \frac{1}{1 - 0.15} (1.1)^{40} - 64.3 - (64.3)(\frac{1}{1 - 0.15} - 1)(1.04)^{40})(1.04)^{-40} = 688.39\) billion dollars in taxable capital gains, which at an estimated average long-term rate of 15% means a loss of $103.26 billion in tax revenue.3 It's worth noting that this is significantly worse than what we get using the naive estimates made by e.g. the internet calculators I linked above, which wouldn't account for the increase in borrowing that a rational investor with a consistent risk appetite would take (the naive estimate results in a present value of \((64.3 \cdot (1 + 0.1)^{40} - 64.3) \cdot (1 + 0.04)^{-40} = 592.76\) billion in capital gains, 15% of which is $88.9 billion in tax savings), but the kicker is that this naive estimate would also estimate that taxpayers benefit to the tune of this 88.9 billion (present value, but assuming contributions and population size are consistent this would also be roughly true in terms of cash on hand) per year, meaning it looks like a wash to the average voter.
Of course, this calculation assumes every Roth IRA investor is rational (it's probably closer to the opposite) and that the only alternative is taxable accounts (so ignores traditional retirement accounts), and it also doesn't consider the wider economic implication that approximately \(64.3 (1 - \frac{1}{1 - 0.15}) = 11.35\) billion additional dollars would be borrowed and invested in the stock market over the course of a year in this scenario (though this probably would not be economically significant, even when considering the resulting increase in business activity). Also, the US government has demonstrated a preference for cash-in-hand over future revenues that far exceeds discounting by the risk-free rate4, so it would be hard to sell legislators on the idea of doing away with it. In actual fact, the existence of the Roth IRA likely benefits taxpayers at an amount closer to the $89 billion figure than the $9 billion one, but most of this is by inducing investors to become more rational by aligning their portfolios more with their actual risk tolerance, not by actually helping out their tax bill. And this result is still a pretty big condemnation of the Roth IRA from a policy standpoint – if Congress axed the program and reduced capital gains rates by whatever percentage the real cost (the number we estimated to be between $89 and $103 billion) would constitute of federal capital gains revenues, even if only a few would-be Roth investors are rational and start adding leverage, the average taxpayer would still benefit. Even if only a negligible number of people currently know to do this, Congress could spend up to $103 - $89 = $14 billion on financial education to convince people to start leveraging after axing the Roth IRA and still break even on the tax revenue increase if everyone who would have held a Roth starts borrowing to invest, let alone investors without a Roth IRA who might be induced to start doing this.
Practical implications
Obviously, it doesn't really matter how a Roth IRA compares to a taxable account as long as it's strictly better, which we have proven that it is5 – any investment that will only be withdrawn after age 59½ is obviously better to put in a Roth than a taxable account, and that holds whether the excess value of the Roth is $0.01 or $1,000,000. However, the idea of using leverage to create an account with similar returns to a Roth IRA has revealed something important: anyone who invests an entire Roth IRA in non-risk-free assets is implicitly accepting a higher level of leverage, and thus a higher level of risk, than what the same portfolio contents invested in a taxable account would represent. This doesn't immediately imply anyone with both a Roth IRA and taxable investments should invest all taxable funds according to the replicating strategy, but it does imply that most people are actually comfortable with a higher level of risk than they implement, and thus would benefit from leveraging up investments.
I mentioned in the first section that principled investors value assets on a risk-adjusted basis. To be clear, leveraged investing for purposes of retirement is not novel, and among economists may even be considered mainstream. This paper, which also inspired a book by its authors, has received mainstream attention for recommending young investors take on over 100% exposure to US stocks6, arriving at their results by proposing the idea of "diversification across time". Moreover, this idea that any portfolio can be leveraged up or down to fall in line with risk preferences once its composition is optimal from a correlation perspective is a cornerstone of the field of portfolio optimization. So why haven't these academic ideas trickled down to retail yet?
To retail's credit, it is not immediately intuitive that an optimal financial strategy could include (implied) debt, especially in the context of borderline predatory margin rates for retail whose alternatives require intricate knowledge of derivatives and the US tax code as well as level 4 options approval (see this article). Also, what little financial education exists often paints a picture of debt informed by objectively undesirable debt like credit cards and payday loans. As leverage can mean a difference of hundreds of thousands to millions of dollars in retirement for average investors, this discrepancy indicates that even relatively-financially-literate people (at least, financially-literate enough to be saving in Roth IRAs) could benefit from increased financial education.
Perhaps more alarmingly, many professional financial advisors and all the "target date" funds7 that I've seen appear to share the same stigma towards leverage, which likely results in suboptimal returns for clients and fund investors. This is probably not a very big issue in practice, because younger investors who could benefit from leverage usually don't have much money invested and are less likely to have financial advisors in the first place. But the problem seems very easy to fix (in some cases, as easy as allowing a "cash" parameter to take on negative values in a portfolio optimizer or Monte Carlo simulator), and firms that aren't afraid of leverage and can explain it to potential clients well enough might be able to draw younger investors due to this gap in the market. This also means that a market may exist for ETFs or hedge funds offering risk-adjusted returns similar to common indices like the S&P 500, just with higher leverage ratios, which might be attractive to investors who either lack access to cheap leverage or irrationally stigmatize (implied) debt unless it is hidden behind the sticker price of a tradable security.
Conclusion
My original purpose for writing this article was mainly to share what I initially believed to be an original observation regarding the fair value of the Roth IRA, as well as to provide an introduction to the idea of no-arbitrage pricing that might interest personal finance or mathematics enthusiasts who largely don't need to care about most applications of it, and which doesn't require a technical background to understand. No-arbitrage pricing is an essential tool in quantitative finance – a companion article to this one discussing implied interest rate opportunities accessible to retail investors makes heavy use of it, for instance – and having an article like this allows me to get straight into the weeds in future articles while directing readers without that background knowledge here first.
Once I started writing, however, I realized it has implications for the somewhat-mathematically-literate reader far beyond a toy example of a useful concept. Once one accepts the premise that a Roth IRA is essentially just a form of free leverage that 18% of Americans willingly contribute to8, the fact that many Americans who would consider themselves financially literate are psychologically averse to even the idea of leverage becomes a striking contradiction with the implicit leverage they adopt via a Roth IRA. Moreover, we've seen that without this contradiction, Roth accounts would be a woefully inefficient tax policy, which has interesting implications regarding the efficiency of capital gains taxes in general. Finally, while the fact that not all market participants act rationally is hardly new to the fields of economics or finance, it is concerning that an irrational aversion to leverage is common to laypeople and financial advisors alike, and the fact that people tend to be less averse to investing in a Roth IRA than levering up by an amount proportional to the capital gains rate is an excellent way of displaying the internal inconsistency of this bias.
Notes and acknowledgements
I "discovered" this valuation method for the Roth IRA independently, and as far as I'm aware, only one other person has realized this and posted it on the internet (well before me), which is this article: https://earlyretirementnow.com/2016/06/07/synthetic-roth-ira/. That article goes more into crunching numbers of the practical implementation details for its author's personal circumstances rather than using it to motivate the theory of arbitrage-free pricing. One other thing to note is that it uses regulated futures, which are subject to Section 1256 rules, rather than synthetic futures on equity-settled options or box spreads. With Section 1256 rules, capital gains taxes are assessed as 60% of long-term rates plus of 40% short-term rates, meaning for example that the top marginal tax rate is 26.8%, not 20% – this is objectively worse than using box spreads, whose implied interest is assessed as a capital loss and thus can offset any capital gains on any arbitrary asset, whether short or long term. It seems the author of that article trades actively in his retirement accounts, in which case the Section 1256 rates are actually preferable to the short-term capital gains rate he would otherwise pay, but in my experience, most retirement investors are passive and would generally be subject to long-term rates, and would thus lose money by using regulated futures instead of box spreads.
Edit: As mentioned in a footnote, portfolio management methods (CAPM/Sharpe ratio) advocating leveraging based on risk have been around for a long time, though they're usually presented in a context without taxes. But while researching for a later article, I noticed that Thorpe 26-27 explicitly mentions the idea that capital gains taxes are worth exactly the cost to leverage them out, though this is only in the context of a log utility function, geometric Brownian returns, and continuous rebalancing (this is somewhat of an oversimplification, see that paper for context).
Footnotes:
Sometimes this merely refers to the use of a geometric mean rather than an arithmetic mean to account for differences in volatility. In this article, while we won't often discuss rate of return per se as it doesn't affect our method of valuation, any "average" returns we quote will be taken to be a geometric average; here, we mean risk-adjusted in a sense more akin to what is found in portfolio optimization.
CAPM/Sharpe ratios also account for this in a somewhat-rigorous way, and some variant of this is usually what people mean when discussing risk-adjusted returns, but in this case we can frame this in a way that captures something more general than a simple mean-variance adjustment (in particular, our "adjustment" works no matter the utility function, while the typical guidance of "Leverage = Sharpe ratio" essentially assumes log utility).
All else being equal, it's arguably slightly better for the IRS if the customer gets a worse rate, as an automated margin loan costs the bank and broker essentially nothing to issue and the spread for both parties is pure profit, so it effectively gets taxed at corporate tax rates (and arguably, the resulting capital gain or dividend for the broker or bank gets taxed at capital gains rates again). The current highest long-term tax rate is 20% while the current corporate tax rate is 21%. If we add the net investment income tax then the long-term gains rate slightly exceeds the corporate income tax for high-income investors, but if we count the implied double-taxation, it's still significantly better for the IRS if investors get bad margin rates. Of course, some of the gain may cause larger bonuses or increased capital expenses for the bank, but then the money eventually gets taxed at income tax rates, etc. The point is, the IRS doesn't lose money when people who would take loans anyway get a worse rate on margin (or a worse deal on any other transaction cost for that matter), and in fact probably gains some from the resulting economic activity.
As many consider T-bills to define the risk-free rate, this is a roundabout way of saying that the US tends to run deficits.
Technically, we have only proven this when the risk-free rate is positive. If it were negative, it would actually be beneficial to borrow the amount required to offset capital gains, so a Roth IRA would be strictly worse than a taxable account (also, humorously, holding cash under a mattress is a prohibited transaction for an IRA, but not in a taxable account). In practice, it's unlikely that rates will ever become substantially negative as many banknotes can be held in vaults and insured at prices that are fairly cheap compared to the value of the notes themselves, so borrowing and insuring banknotes would be an arbitrage opportunity and thus be executed in so much volume that the cost of lending money would rise to no more than the cost to maintain and insure a vault containing it. Arbitrage-free pricing strikes again!
This is not to say that investors with some proportion of stock and some proportion of bonds cannot also benefit from leverage; indeed, most corporate bond indices have average year-over-year returns exceeding the implied interest rate of box spreads, so these can also benefit from increased leverage. On the other hand, any portfolio with any allocation to cash in bank accounts, short-term CDs, or money market funds essentially already has less than 100% leverage, as such assets historically return approximately the risk-free rate.
One could still use leverage to buy shares of a target date fund (which holds no cash) and decrese the leverage over time manually, which likely approximates an optimal retirement strategy, but this is not the "set-it-and-forget-it" experience advertised by most target date funds.
It's possible some keen arbitrageurs or even risk-averse retirees among them use their Roth to buy T-bills, but I'd wager that's not most of them.