Kelly-Optimal Options Positions
Table of Contents
The ideas of risk-neutral pricing and modeling asset returns with stochastic processes for purposes of derivatives pricing have lead to an explosion of liquidity in derivative contracts. Even in the absence of fundamental or technical information on the underlying securities, market makers can and do use such mathematical models to value these products. Yet, for every derivatives market maker, there are thousands of traders in such contracts who buy them because they believe their own research, or occasionally inside information, gives them an edge in predicting the price movements of the underlying security. This article aims to examine how traders who believe themselves to be knowledgeable about the future returns of an asset, and who have a specific set of utility preferences, should use options to optimally profit from this knowledge in both ideal real-world markets.
In this article, we'll model research/information as yielding a belief about the probability measure governing asset returns. The Breeden-Litzenberger formula then allows us to view the options market as a game of chance where some bets are favorably-priced, on which the optimal way to speculate is a solution to an optimization problem in terms of the trader's utility function. We will explore the merits of using logarithmic utility, also known as the Kelly criterion, and discuss some senses in which it is optimal. Then, we'll show that in complete markets, the optimal options spread has an interpretation as a relative entropy maximizer. In incomplete markets, the Kelly-optimal positions in the available set of derivatives contracts can be found with a convex optimization problem involving numerical integration (necessary for arbitrary probability densities), and can be viewed as a constrained version of the complete case. In the presence of a bid-ask spread, more constraints are added, and with finite increments, it becomes an integer programming problem. Finally, we implement our results on real S&P 500 options data, then give a polynomial approximation method that can speed up the optimization problem for a wide class of parametric probability measures.
Definitions and Notation
Let \(\Omega\) be a sample space and \(\{\mathcal{F}_t\}_{t \geq 0}\) a filtration on \(\Omega\). We'll write \(F_t\) to mean any particular \(\mathcal{F}_t\)-measurable set containing all events compatible with a trader's observations at time \(t\) in some sampling of this process. First, all results in this article will assume a universe with a constant risk-free log-interest rate \(r\), at which traders can both borrow and lend unlimited amounts of money such that money lent at \(t_1\) will be worth \(e^{r(t_2 - t_1)}\) at \(t_2\). We're focusing on the case where a trader has knowledge about one particular security \(S_t: \Omega \to \mathbb{R}_{\geq 0} \) which is a \(\mathcal{F}\)-adapted semimartingale, and is attempting to profit (on an \(r\)-discounted basis) by trading in \(S\) and its European options chain. For convenience, we'll say \(S_0 = 1\), so that \(S_t\) represents the arithmetic rate of return at time \(t\) for an investor who has been long in \(S\) since time 0. We will write \(\sigma(S_{T}\) to mean the σ-algebra generated by \(S_T\), which is a sub-σ-algebra of \(\mathcal{F}_T\).
In this article, we'll start off with "ideal" market conditions, which we define to mean:
- Completeness: For all \(t \geq 0\) and all \(\mathcal{F}_t\)-measurable random variables \(X\), there is a security tradable (at prices dictated by the market) until time \(t\) which at time \(t\) is worth \(\$X\) (an "\(X\)-European contingent claim")1. A market which is complete with respect to a sub-σ-algebra \(\mathcal{G} \subseteq \mathcal{F}\) will be referred to as \(\mathcal{G}\)-complete.
- Perfect liquidity: Every tradable security can be bought and sold at the same price (in arbitrarily-large quantities).
- Arbitrary increments: Every tradable security can be bought and sold in arbitrarily-small increments.
And as the article progresses, we will progressively remove these assumptions.
This article assumes some familiarity with vanilla options contracts; a section in an earlier article of mine gives some basic explanations of what they are and how someone would want to use them. As this article is primarily concerned with profiting from existing options prices rather than attempting to independently value them, we won't need to write the premium and intrinsic value at expiry separately except for in a small introductory portion. Thus, going forward, when we refer to an instrument's "payoff", we're referring to its \(r\)-discounted payoff function, including any premiums if applicable. We'll write \(C^{(t, T)}_K: \mathbb{R}_{\geq 0} \to \mathbb{R}\) to mean the payoff for the buyer of a call option at strike \(K\) purchased at time \(t\) and expiring at time \(T\), and call the payoff for the buyer of the corresponding put \(P^{(t, T)}_K\). That is to say, if the call option with strike \(K\) expiring at time \(T\) is trading at premium \(c\) at time \(t\), then \[C^{(t, T)}_K (S_T) = e^{r(t - T)} (S_T - K)^+ - c\] where we write \((\cdot)^+\) to mean \(\max (0, \cdot)\). Note that \(-C^{(t, T)}_K(0)\) (resp. \(-P^{(t, T)}_K(\infty)\)) is always equal to the call (resp. put) premium, so we'll use these to refer to premiums going forward. Also note that the return of a call with strike zero is equivalent to that of a long position in the underlying, and as \(K \to \infty\), the return of a put at strike \(K\) approaches the return of a short position pointwise, so we will henceforth refer to the returns of long and short positions as \(C^{t, T}_0\) or \(-P^{t, T}_\infty\) and \(P^{t, T}_\infty\) or \(-C^{t, T}_0\) respectively.
This notation enables us to express the payoff of an investor's position in an entire options chain quite concisely. If \(E\) is the set of strikes at which options are offered (\(\mathbb{R}_{\geq 0}\) in a complete market), we can view \(C^{(t, T)}\) and \(P^{(t, T)}\) as vectors in \((\mathbb{R}_{\geq 0} \to \mathbb{R})^E\), which has a natural embedding in \(\mathbb{R}_{\geq 0}^E \to \mathbb{R}^E\), so that in particular, \(C^{(t, T)}(S_T) \mid F_t\) and \(P^{(t, T)}(S_T) \mid F_t\) are \(\mathbb{R}^E\)-valued random variables. Then if \(\alpha_K\) is the number of calls at strike \(K\) an investor buys (if negative, sells) at time \(t\), with \(\beta_K\) analogous for puts, the investor's discounted excess returns are simply \[\alpha \cdot C^{(t, T)}(S_T) + \beta \cdot P^{(t, T)}(S_T).\]
The Kelly Criterion: From Blackjack and Horse Racing to Black-Scholes and Heston
Options Prices are Odds: The Breeden-Litzenberger Transformation
As mentioned in the introduction, traders' beliefs about the time-\(T\) state of the market, including the price of some tradable security, can be modeled as a probability measure over \(\mathcal{F}_T\), say \(P_T: \mathcal{F}_T \to [0, 1]\). Derivatives prices also reflect market opinion about a probability measure. According to the famous result of Breeden and Litzenberger, in ideal markets, there is a bijective relationship between the set of possible arbitrage-free2 vanilla options chains on an asset \(S\) and the set of equivalent (i.e. mutually absolutely continuous with the "true" underlying measure) local martingale (i.e. under which all tradable assets' \(r\)-discounted payoffs, including premiums, are local martingales) measures over \(\sigma(S)\). In particular, for any particular time \(T\), each options chain with expiry at time \(T\) is compatible with exactly one equivalent martingale measure over \(\sigma (S_T)\), which we'll call \(Q_T\), characterized by the fact that \(S_T\)'s density under \(Q_T\) equals \(-e^{rT} \frac{d^2C^{(0, T)}_K(0)}{dK^2}\), the second derivative of its call premiums with respect to strikes times \(e^{rT}\), almost surely.
As it turns out, the explicit formula for \(Q_T\) in terms of vanilla options prices isn't very useful (at least for our purposes), so we relegate the proof to a footnote3. In markets where the set of tradable strikes are not dense, the second derivative of call premiums with respect to strikes isn't well-defined. In \(\sigma(S_T)\)-complete markets, \(Q_T(A)\) could be directly found as the premium of the European contingent claim associated with \(\chi_A\), the indicator function for any event \(A \in \sigma (S_T)\).
In fact, the latter case is more or less the complement of the former: for open intervals \((x, y)\), each \(S^{-1}((x, y))\)-European contingent claim is the limiting case of constructing iron condors by buying puts at strike \(a - \delta\), selling puts at strike \(a\), selling calls at strike \(b\), and buying calls at \(b + \delta\) as \(\delta \to 0\) (with the number of contracts such that the sum of premiums is 1). Note that "synthetic puts", which mimic the returns of real puts, may be constructed by combining a call \(C_K^{(t, T)}\) and a short position \(-C^{(t, T)}_0\), so all we really need is calls (and vice versa, if we only wanted to use puts). This of course implies such a dense set of calls is enough to replicate any \(\sigma(S_T)\)-measurable European contingent claim arbitrarily-well (in any \(L^p\) sense) due to the definition of the Lebesgue sets and density of such indicators in the space of \(\sigma(S_T)\)-measurable random variables, and the limit of the sum of premiums of such a sequence of approximating strategies for some \(\chi_A\) would likewise equal \(Q_T(A)\). So in markets with a continuum of strikes, by trading "close enough" approximating strategies, all \(\sigma(S_T)\)-measurable European contingent claims are for all practical purposes tradable.
In this sense, an options position is essentially specifying some amount to wager on whether or not events in \(\sigma(S_T)\) occur. The "odds", or the payouts for correct "wagers", are dictated4 by the equivalent martingale measure: by definition, every \(\sigma(S_T)\)-measurable European contingent claim's payoff is a martingale under this measure, so the premium for \(\chi_A\)'s European contingent claim is \(\mathbb{E}^{Q_T}[\chi_A] = Q_T(A)\) and its payoff function is \(\chi_A - Q_T(A)\). But unless our trader's measure \(P_T\) is identical to \(Q_T\) on \(\sigma(S_T)\), there is some \(A \in \sigma(S_T)\) whose real probability is believed by the trader to be \(P_T(A) \neq Q_T(A)\), and thus the trader's expected value from going long one unit of the bet is \(\mathbb{E}^{P_T} [ \chi_A - Q_T(A) ] = P_T(A) - Q_T(A)\); the trader should clearly go long or short on this bet according to whether this is positive or negative.
This situation is reminiscent of a card counter betting on blackjack who believes the distribution of undealt cards implies an expected profit, or a professional gambler who believes some horses have better chances of winning a race than their odds as posted by the bookies, with the only difference being that the σ-algebra is not discrete. Indeed, this next section will apply to any game with a set of possible bets of which some are submartingales, and can be directly applied to vanilla options without the above formulation as indicator functions, but we'll see that the indicator formulation provides insight into how \(Q_T\) "sets" the odds.
Moreover, let's for the moment suppose our trader expects to have tradable knowledge fairly often, analogous to a card counter who can play many advantageous hands of blackjack, and that this trade's potential profit is roughly representative of that of future knowledgeable trades – we'll discuss the (un)importance of this assumption later.
A Log-ical Way to Gamble
One intuitive way for our trader/gambler to proceed is to maximize the expected returns after some number of bets \(n\) on the same game/options chain, i.e. taking \((\alpha, \beta) = \arg \max_{(\tilde{\alpha},\tilde{\beta})} \mathbb{E}^{P_T} \left[ \left( \tilde{\alpha} \cdot C^{(t, T)}(S_T) + \tilde{\beta} \cdot P^{(t, T)}(S_T) \right)^n \mid F_t \right]^{\frac{1}{n}} \). Unfortunately, this is likely to be unsatisfactory for large \(n\) because it views losing one dollar the same whether one has \$1 million or has only that single dollar remaining, and thus is likely to quickly go bankrupt. In fact, readers with an analysis background will recognize that as \(n \to \infty\), this expectation converges to the \(L^\infty\)-norm, or the largest value attained by \(\tilde{\alpha} \cdot C^{(t, T)}(S_T) + \tilde{\beta} \cdot P^{(t, T)}(S_T)\) with a nonzero probability – in other words, for large enough \(n\), the solution to the optimization problem only depends on the best-case scenario, which doesn't seem like a great way to make decisions! The discrete case provides intuition for why this is – in the horse race analogy, it clearly follows from linearity of expectation that if the expected return from betting $1 on one horse is higher than that of all others, the same holds for any dollar amount, and one should therefore bet all one's money on this horse. Of course, if that horse wins with probability \(h < 1\), after \(n\) of the same race, the gambler loses everything with probability \(1 - h^n\), which approaches \(1\) as \(n \to \infty\).
If we're uncomfortable with being overwhelmingly likely to lose our entire investment in order to maximize expected returns, this is a good indication that we have a concave utility function, which is to say that our value of an additional dollar decreases as our wealth increases. One sensible concave utility function is the natural logarithm, which as a utility function is often known as the "Kelly criterion". Logarithmic utility functions have been around for a long time, at least since Daniel Bernoulli's proposed solution to the St. Petersburg Paradox, but a proposal of John Kelly in 1956 to use this utility function and his observation that it results in wager amounts of one's wealth proportional to a bet's expected returns for bets on favorable coin tosses and horse races (we'll later see a continuous analog) birthed the name.
Later authors proved that it is "optimal" in several senses, most notably that among any strategy wagering a fixed fraction of one's wealth on successive iterations of the same event, as the number of iterations approaches infinity, the probability that a gambler following the Kelly-optimal strategy has more wealth than a gambler with the same initial wealth following any other fixed-fraction strategy approaches 1. A survey of other senses in which the Kelly criterion is optimal is given here.
Another reason we choose to use logarithmic utility is that it is isoelastic, which is to say that percentage changes in one's wealth affect utility the same amount regardless of the original magnitude of one's wealth, i.e. that rich and poor people both value percentage changes in their wealth equally. This is a trivial consequence of the "log rule" that \(\log(ab) = \log(a) + \log(b)\): if one's wealth is \(a\), the additive utility of an event causing wealth to be multiplied by \(b\) clearly does not depend on \(a\). Whether this is realistic largely depends on individual investor preferences, but this is an assumption large corporations whose shareholders have diverse wealths are essentially forced to make, and it has the added benefit of making models scale-invariant.
Isoelasticity also implies that the number of times a bet is offered doesn't affect optimal wager sizes: after \(n - 1\) iterations of betting, since our current wealth doesn't affect the proportion of it we bet, we will bet the same fraction as in the 1-iteration case regardless of the outcomes of the earlier bets, and the rest follows by induction. So if we had assumed logarithmic utility from the start, our earlier assumption that we will be offered a large number of roughly similar games would not have mattered, though such an assumption is still necessary for the optimal limiting properties distinguishing the logarithm from other isoelastic utilities to be meaningful. In fact, empirical studies of risk aversion have shown that humans tend to favor more risk-averse isoelastic utility functions. Such functions are not even computationally intractable if used in the same ways as the logarithm below, and these will likely be a topic of future articles on this site, but this article only deals with logarithmic utility for simplicity.
Back to Options: "Perfect" Markets
Now that we have a utility function, we can maximize its expected value over all possible options positions. We could of course do this by maximizing \[\mathbb{E}^{P_T} \left[ \log \left( \hat{\alpha} \cdot C^{(t, T)}(S_T) + \hat{\beta} \cdot P^{(t, T)}(S_T) + 1 \right) \: \middle\vert \: F_t \right]\] over all possible positions \(\hat{\alpha}, \hat{\beta}\) directly (the \(+ 1\) is for our current wealth, which we define as one "unit"; our options payoff functions already included premiums and discounted with respect to \(r\), so our positions in those only convey gains/losses, not our starting wealth). However, a position in multiple options is equivalent to a European contingent claim whose payoff is the sum of the payoffs of the options, and we proved above that options at a dense set of strikes allow us to approximate the payoff of any \(\sigma(S_T)\)-measurable European contingent claim arbitrarily well. So this problem is also equivalent to maximizing \[\mathbb{E}^{P_T} \left[ \log \left( X^{(t, T)} + 1 \right) \: \middle\vert \: F_t \right]\] for \(X\) in the set \(\mathcal{X}\) of all \(\sigma(S_T)\)-measurable European contingent claim payoffs such that \(P_T(X > -1 \mid F_t) = 1\).
How can we characterize this set? In complete markets, every \(\sigma(S_T)\)-measurable random variable is the time-\(T\) value of some tradable contingent claim, and all contingent claims are valued under \(Q\) such that they are martingales and their payoffs have 0 expected value at any time. Thus \(\mathcal{X} + 1\) (elementwise) is just the set of positive \(Q\)-martingales whose \(Q_T\)-expected value is 1. This is exactly the set of possible Radon-Nikodym derivatives of probability measures with respect to \(Q\)! Indeed, clearly \(R_X(A) := \int_A X dQ \) is a probability measure for any such \(X\), and for any \(R \ll Q\) and \(t\), we have \(\mathbb{E}^{Q} \left[ \frac{dR}{dQ} \mid \mathcal{F}_t \right] = \mathbb{E}^{R} \left[ 1 \mid \mathcal{F}_t \right] = 1 \ \text{a.s.}\).
This may seem like it comes out of nowhere, but it's actually a very natural corollary of the discrete case and the Lebesgue differentiation theorem. Recall the case of an indicator contingent claim for some event \(A\), and suppose we partition \(\mathbb{R}_{\geq 0}\) into a finite number of half-open intervals \(A_1 \ldots A_n\). Further suppose our trader may allocate our initial wealth 1 among the claims with payoffs \(\frac{\chi_{A_i} - Q_T(A_i)}{Q_T(A_i)} = \frac{\chi_{A_i}}{Q_T(A_i)} - 1\) for \(i = 1 \ldots n\) (indicators normalized so that betting 1 on any claim risks all initial wealth), with "selling" modeled as "buying" \(A_i^C\) rather than its own transaction. Since the allocations sum to one, they can be naturally extended into a probability measure over the set of unions of the \(A_i\)s (where each union's measure is the sum of the measures of the members). Call this measure \(R_T\). Then the trader's final wealth is \[1 + \sum_{i = 1}^{n} \chi_{A_i} \left(\frac{R_T(A_i)}{Q_T(A_i)} - 1 \right) = \sum_{i = 1}^{n} \chi_{A_i} \frac{R_T(A_i)}{Q_T(A_i)}.\] By a trivial consequence of the Lebesgue differentiation theorem, we have that \(y_n, z_n \to 0\) as \(n \to \infty\) implies \(\lim_{n \to \infty} \frac{R([x - y_n, x + z_n))}{Q([x - y_n, x + z_n))} = \frac{dR}{dQ}\). So modeling the final wealth as a Radon-Nikodym derivative is in this sense the limiting case of all-or-nothing bets on a finite number of outcomes.
Thus, the optimization problem can be rewritten as \[ \mathop{\text{arg} \, \text{max}}_{R_T \text{ a probability measure on } \sigma(S_T)} \mathbb{E}^{P_T} \left[ \log \left( \frac{dR_T}{dQ_T} \right) \: \middle\vert \: F_t \right].\] Readers familiar with information theory will recognize that the solution is \(R_T = P_T\), where the value of the objective function equals the Kullback-Leibler divergence \(D_{KL}(P_T \: \Vert \: Q_T)\).5 In fact, the solution to the optimization problem (though not the optimal quantity) doesn't even depend on \(Q_T\)! Indeed, \[\log \left( \frac{dR_T}{dQ_T} \right) = \log \left( \frac{\frac{dR_T}{dP_T}}{\frac{dQ_T}{dP_T}} \right) = \log \left( \frac{dR_T}{dP_T} \right) - \log \left( \frac{dQ_T}{dP_T} \right), \] and the second term is constant in \(R_T\), so the optimizer equals \[ \mathop{\text{arg} \, \text{max}}_{R_T \text{ a probability measure on } \sigma(S_T)} \mathbb{E}^{P_T} \left[ \log \left( \frac{dR_T}{dP_t} \right) \: \middle\vert \: F_t \right]. \] The problem is thus equivalent to maximizing \(D_{KL}(R_T \: \Vert \: P_T),\) which is equivalent to \[ \mathop{\text{arg} \, \text{max}}_{R_T \text{ a probability measure on } \mathbb{R}_{\geq 0}} \mathbb{E}^{P_T \circ S_T^{-1}} \left[ \log \left( \frac{dR_T}{dm} \right) \: \middle\vert \: S_T(F_t) \right], \] the usual definition of cross-entropy from \(R_T\) to \(P_T\), by properties of the KL divergence. Here, composing \(P_T\) with \(S_T^{-1}\) is used to view \(S_T\)'s possible returns, rather than \(\Omega\), as the underlying probability space, so that we can use the Lebesgue measure (as \(\Omega\) need not have the same sort of "canonical" measure). So we have shown that finding the optimal position is equivalent to a cross-entropy minimization problem.
Real-World Approximations
Of course, options in the real world aren't offered at a dense set of strikes, have significant bid-ask spreads, and often have fairly large minimum increments. We'll see that as we remove each of these assumptions, each new problem essentially becomes a more constrained version of the last. For purposes of this section, we'll again assume the trader has some probability measure over \(\mathcal{F}_T\), without loss of generality assuming \(T = 1\), but may only trade at a single (fixed) prior time, which we assume without loss of generality to be 0. Thus, we can simplify notation and write \(P = P_1\), similar for other measures. We'll also relax this last assumption a little later and see that the methods developed here are still useful.
Incomplete Markets
The results of the last section – in particular, the fact that we can optimize expected utility without even considering \(Q\) – implies that we don't even need to know the prices of derivatives contracts at all in order to optimize our position. If we could apply this to real-world market conditions, it would greatly simplify mathematical models informing trades, and high-frequency traders wouldn't even have to wait for (or even pay for) price quotes anymore!
We Need to Look at Prices After All
There are two primarily problems with applying the previous section's findings when options are traded at a finite number of strikes. First and foremost, we can no longer choose \(R\) to be any probability distribution – it may only be chosen among those formed as linear combinations of tradable option payoffs. Second, we can no longer approximate indicator contingent claims arbitrarily well, and the idea of a second derivative with respect to strikes doesn't even make sense, so we can no longer find a unique equivalent martingale measure.
Luckily, we found a way to write our optimization problem without using the equivalent martingale measure above, so it seems like we won't have to worry about choosing (and computing) a specific \(Q_1\). However, the first issue changes the optimization problem to something like \[\mathop{\text{arg} \, \text{max}}_{R_1 \text{ a probability measure expressing an options position}} \mathbb{E}^{P_1 \circ S_1^{-1}} \left[ \log \left( \frac{dR_1}{dm} \right) \right],\] and it's not immediately clear what that constraint on \(R_1\) even means. Unfortunately, while \(\frac{dR_1}{dm}\) doesn't depend on \(Q_1\), the set \(\mathcal{R}\) satisfying the constraint does! Recall that in the last section, we explicitly defined \(\frac{dR_1}{dQ_1} = X + 1\), where \(X\) was the payoff of the contingent claim representing our returns – in this case, it's just \(\alpha \cdot C^{(0, 1)} + \beta \cdot P^{(0, 1)}\), and thus \[\mathcal{R} = \left\{ R \ \middle\vert \: \frac{dR}{dQ} = \left( \alpha \cdot C^{(0, 1)} + \beta \cdot P^{(0, 1)} + 1 \right) \text{ and } \alpha \cdot C^{(0, 1)} + \beta \cdot P^{(0, 1)} > -1 \mathop{\text{a.s.}} \right\}\] where the second condition is arguably redundant if we enforce that \(\mathcal{R}\) may only contain probability measures.
This essentially forces us to fall back to the first statement of the optimization problem in terms of \(\frac{dR}{dQ}\), which is also the approach we would end up using even if we didn't bother observing the information-theoretical connection. That is to say, our problem has become
\begin{align*} \arg \max_{(\alpha,\beta)} \mathbb{E}^{P} \left[ \log \left( \alpha \cdot C^{(0, 1)}(S_1) + \beta \cdot P^{(0, 1)}(S_1) + 1 \right) \right] \\ \mathop{\text{s.t.}} \: \alpha \cdot C^{(0, 1)} + \beta \cdot P^{(0, 1)} > -1 \end{align*}Actually, under the fairly weak assumptions that there are two different tradable strikes (one of which can be 0, so long/short positions) and \(m \ll P\) at all option break-even points6, we can even drop the constraint if we only consider the real part, i.e. if we change the problem to \[\arg \max_{(\alpha,\beta)} \mathbb{E}^{P} \left[ \log \left( \vert \alpha \cdot C^{(0, 1)}(S_1) + \beta \cdot P^{(0, 1)}(S_1) + 1 \vert \right) \right].\] To see why, assume for contradiction that some optimizer of this new version version \(\alpha, \beta\) violates \(\alpha \cdot C^{(0, 1)} + \beta \cdot P^{(0, 1)} + 1 > 0\). The payoff function is a linear combination of continuous functions, and thus is itself continuous. Moreover, it integrates to 1, so by Markov's inequality attains a value at least 1. Thus, by intermediate value theorem, there is some \(x\) at which \(\alpha \cdot C^{(0, 1)}(x) + \beta \cdot P^{(0, 1)}(x) + 1 = 0\). Furthermore, it's clear that the payoff function is \(L\)-Lipschitz for some \(L \leq |\alpha| + |\beta|\). Now, via Leibniz's integral rule, we compute the gradient of the objective function to be \[\int_0^\infty \begin{bmatrix} C^{(0, 1)}(x) \\ P^{(0, 1)}(x) \end{bmatrix} \frac{dP \circ S_1^{-1} (x)}{dm} \frac{1}{|\alpha \cdot C^{(0, 1)}(x) + \beta \cdot P^{(0, 1)} + 1|}dm(x)\] (where the vector means \(C^{(0, 1)}(x)\) and \(P^{(0, 1)}(x)\) stacked on top of each other). Since any two calls or puts at different strikes have different break-even points and \(m \ll P\) at all of them, letting \(\delta\) be such that not all break-even points lie within \((x - \delta, x + \delta)\), the absolute value of dimension \(K\) of this integral over \((x - \delta, x + \delta)\) is at least \[\left(\min_{d \in (-\delta, \delta)} \left(|\frac{dP}{dm}(x + d) C_K(x + d)|\right)\right)\int_{-\delta}^{\delta} \frac{1}{|Ly|} dm(y),\] which diverges, so the gradient cannot be zero at the optimum, which is a contradiction.
Note also that if we assume long/short positions are encoded as 0-strike calls but not as ∞-strike puts, at least some (global) optimum will satisfy \[ \alpha_K > 0 \ \forall K \in E, \]
that is, it will not sell any calls. This fact will be useful in future sections. To see why it is equivalent, first observe that if the number of calls sold exceeds the number of calls bought, the payoff function will be strictly decreasing in \(S_T\) when \(S_T\) exceeds the largest strike offered, and thus will eventually become negative, which we proved above cannot be optimal. Now, suppose a call is bought at strike \(K_1\) and another is sold at \(K_2\). One can easily verify that these could be replaced by buying a put at \(K_2\) and selling a put at \(K_1\), with no impact to the payoff function.
Note also that a long position and a short put can create a "synthetic long call" which could theoretically replace the rest of the long calls, too, but there is less reason to do this (whereas short calls are bad for numerical stability because they can in practice cause negative values of the objective function at very high underlying prices due to the probability density function being possibly very low there).
Insights from the information-theoretical interpretation
It's nice that this problem is still tractable, but it's a bit disappointing that we weren't able to use the information-theoretical interpretation we found in the last section. Did we even gain anything from that analysis?
Actually, have found an interesting way to evaluate how incomplete a market is. Recall that the optimal value of the objective function, which is the expected geometric growth rate of wealth, in the unconstrained (complete markets) case was \(D_{KL}(P \: \Vert \: Q)\). By optimizing \(R\) with respect to the objective function, then estimating \(Q\) (how to do this is out of scope for this article) and computing \(D_{KL}(P \: \Vert \: Q)\), we can put numbers on both the expected geometric returns of the best possible real-world strategy and the best possible strategy in an ideal market.
Moreover, if we lived in a world with many independent underlying securities and had views (probability measures) over all of them, estimating \(D_{KL}(P^{(i)} \: \Vert \: Q^{(i)})\) for each different security \(i\) could give us some idea of which optimization problems into which to invest marginal computing power. If we have an options position that's very close to optimal for a particular security, and we assume the others have similarly complete markets, we'd seemingly benefit more from an iteration of gradient descent on one of the others. This breaks down somewhat if the securities may be arbitrarily coupled, but an alternate version including information about the copula could be an area of further research.
Significant Bid-Ask Spreads
Now, we'll consider the case where bid-ask spreads are significant. We'll start by assuming there is infinite liquidity at bid and ask prices, but that they are not equal. Under these assumptions, we now need two "option payoff vectors" for each vanilla option, one for buying and one for selling, assessed at the ask and bid prices respectively (assuming a purely liquidity-taking strategy). Let's call \(\hat{P}\) and \(\check{P}\) the buying and selling versions respectively, similar for calls, and we'll drop the superscript \((0, 1)\) (there's no ambiguity with the probability measure \(P\) anymore). Then the problem becomes
\begin{align*} \arg \max_{(\alpha,\beta)} \mathbb{E}^{P} \left[ \log \left(\hat{\alpha} \cdot \hat{C}(S_1) + \hat{\beta} \cdot \hat{P}(S_1) + \check{\alpha} \cdot \check{C}(S_1) + \check{\beta} \cdot \check{P}(S_1) + 1 \right) \right] \\ \mathop{\text{s.t.}} \hat{\alpha}, \hat{\beta}, \check{\alpha}, \check{\beta} > 0. \end{align*}It seems like we should be able to use our discovery that we don't need to sell calls to get rid of \(\check{C}\) and \(\check{\alpha}\), which would at minimum reduce our computations required per iteration by a quarter. In general, we might not be able to: even if we can construct the same position using only calls for cheaper than only puts (or vice versa), bid-ask spreads could be large enough as to deny us an arbitrage because it might be too expensive to short the more expensive one. However, if we assume that \(\hat{C}_0 = \check{C}_0\) (i.e. that the futures contract and/or underlying instrument has negligible bid-ask spread, which is typical of options markets on individual equities), put-call parity dictates that if market makers behave rationally, the spread should have the same effect for calls and puts at the same strike (otherwise they would be offering a synthetic call for cheaper than an ordinary call, or vice versa). So in such markets, we can get away with solving
\begin{align*} \arg \max_{(\alpha,\beta)} \mathbb{E}^{P} \left[ \log \left(\hat{\alpha} \cdot \hat{C}(S_1) + \hat{\beta} \cdot \hat{P}(S_1) + \check{\beta} \cdot \check{P}(S_1) + 1 \right) \right] \\ \mathop{\text{s.t.}} \hat{\alpha}, \hat{\beta}, \check{\beta} > 0. \end{align*}Either way, now that we've seen how to proceed when there is infinite liquidity at the bid-ask spread, it becomes trivial to adapt the problem to a deep order book with finite liquidity at a number of different bid and ask ticks – we simply add more position vectors and constraints (including constraints on the maximum number of transactions at a particular tick) until we run out of orders, or until we don't think we feasibly have the liquidity to exhaust them.
This does increase complexity as the number of ticks we need increases for most numerical optimization methods, but not inordinately; the gradient remains quite tractable, and the ~20 useful strikes and ~5 useful ticks each way characteristic of even the most liquid options chains should only result in a \(400 \times 400\) Hessian at most. Moreover, we'll see later that on real-world data, the bottleneck is usually numerically approximating the Hessian rather than inverting it, so the complexity for using the Hessian is quadratic in the number of ticks rather than being governed by the complexity of matrix inversion (somewhere between quadratic and cubic).
We also observe that while the objective function has been modified when we write it in this way, this can still just be viewed as another constraint on the set of measures encoding our "wagers" with the same objective function as in the complete market case, with the caveat that some may now integrate to less than 1. Even with the more practical way to write the objective function, the incomplete markets case could simply be viewed as a special case of the objective function when \(\hat{C}_0 = \check{C}_0\) and \(\hat{P}_0 = \check{P}_0\). This supports the idea that imperfect markets can be viewed as constraining the space of possible strategies rather than changing market dynamics altogether.
In light of this, we may once again attempt to compare our optimal expected geometric growth rate in the case of significant bid-ask spreads compared to \(D_{KL}(P \: \Vert \: Q)\) to get some idea of how "imperfect" the market is with respect to our preferences. However, one should note that the assumption of significant bid-ask spreads again adds further freedom to how we choose \(Q\).
Significant minimum increments
Now, suppose that in addition to having a bid-ask spread, options contracts are only available in discrete increments. Then the above constrained optimization problem with arbitrary increments is a relaxation of the discrete-increment problem, so a numerical optimization of this relaxation can be run until convergence and the optimum converted to discrete increments via randomized rounding. We won't go into implementation details as code can be found in the implementation section, but vanilla randomized rounding (based on relative coordinate-wise distances from the nearest grid points) will work fine here.
Obviously, smaller increments (meaning larger initial wealth, since contract multipliers for options are generally fixed) result in returns can be to the relaxed optimum. Also, care must be taken to ensure the rounding doesn't result in a position that could possibly lose more than one's initial wealth, which is theoretically possible for large increments. But assuming the randomized rounding gives a position with objective function not too far from the optimal one for this integer programming problem, our subjective heuristic of comparing the result to our theoretically-optimal geometric growth rate \(D_{KL}(P \: \Vert \: Q)\) is still meaningful, it just now also depends somewhat on our initial wealth.
Numerical Implementation and Results
Now that we understand what the optimization problem for finding the optimal options position looks like, let's have a go at implementing it using some real-world CBOE SPX options data (European-style options tracking the S&P500). We'll use the Julia programming language. This section will be a little less formal/polished than the theoretical part, as it's a programming walkthrough that doesn't attempt to be mathematically rigorous.
Setting Up the Environment
This is essentially just some downloads (if needed) and imports.
using Pkg
Pkg.add("YFinance")
Pkg.add("DataFrames")
Pkg.add("Distributions")
Pkg.add("Plots")
Pkg.add("CSV")
Pkg.add("Integrals")
Pkg.add("Random")
Pkg.add("Optim")
Pkg.add("JuMP")
Pkg.add("JSON3")
Pkg.add("BlackBoxOptim")
using YFinance, DataFrames, Distributions, Plots, CSV, LinearAlgebra, Integrals, Random, Optim, JuMP, JSON3, Interpolations, Dates, BlackBoxOptim
Acquiring and Processing Data
There's a package for Julia called YFinance (similar to, but distinct from, the python package) that easily allows us to get options data from Yahoo Finance. This won't give us historical data, only 15-minute delayed quotes, but that should be all we nee for demonstration purposes. We'll use options on the S&P500 index. We can get this data like so:
esputs=DataFrame();
escalls=DataFrame();
if (isfile("esputs.csv") && isfile("escalls.csv") && isfile("esquotesummary.json"))
esputs = DataFrame(CSV.File("esputs.csv"));
escalls = DataFrame(CSV.File("escalls.csv"));
esquotesummary = JSON3.read("esquotesummary.json");
else
esopts = get_Options("^SPX");
escalls = DataFrame(esopts["calls"]);
CSV.write("escalls.csv", escalls);
esputs = DataFrame(esopts["puts"]);
CSV.write("esputs.csv", esputs);
esquotesummary = get_quoteSummary("^SPX");
open("esquotesummary.json", "w") do f
JSON3.pretty(f, JSON3.write(esquotesummary));
end;
end;
return (esputs, escalls)
This data contains a lot of strikes where the bid or ask is very small or the difference between the two is very big – we can remove these as they're not a good reflection of the actual price:
#Filter out strikes where the bid-ask spread is more than 15% of the ask price, or where the bid price is 0, or too far in the money ctemp = select(escalls[map((x) -> !ismissing(x) .& x, ((escalls.ask .- escalls.bid)./escalls.ask .< 0.15) .& (escalls.bid .> 0) .& (escalls.strike .> 5300)), :], :strike, :bid, :ask); ptemp = select(esputs[map((x) -> !ismissing(x) .& x, ((esputs.ask .- esputs.bid)./esputs.ask .< 0.15) .& (esputs.bid .> 0) .& (esputs.strike .< 6500)), :], :strike, :bid, :ask); #const ess0 = esquotesummary["price"].regularMarketPrice #This didn't work well because the price quote was 15 minutes off the options data. So I manually added a rough price and bid-ask spread from that time. const ess0 = 5662.8 const ess0a = 5663.2 const ess0b = 5662.4 return nothing
Finally, we also need to assume some parameters about the market, particularly interest rates. We'll just use SOFR for simplicity – at the time of writing, that's around \(5%\) in archaic annualized daily simple interest terms, and these options have 5 days to expiry, which means our discounting factor is \((1 + \frac{0.05}{365})^5 \approx 1.00027 \). We'll also use this to remove any static arbitrages stemming from put-call parity (Yahoo finance data somehow actually has some)
const disc = 1.00027
#Remove (some, not guaranteed to be all) static arbitrages
badstrikes = intersect(ctemp.strike, ptemp.strike)[.!vec(stack([(ctemp[ctemp.strike .== s, :ask] .- ptemp[ptemp.strike .== s, :bid] .+ s .>= ess0b*disc) .&
(ctemp[ctemp.strike .== s, :bid] .- ptemp[ptemp.strike .== s, :ask] .+ s .<= ess0a*disc) for s in intersect(ctemp.strike, ptemp.strike)]))]
pre_escss = ctemp[.!in.(ctemp.strike, Ref(badstrikes)), :]
pre_espss = ptemp[.!in.(ptemp.strike, Ref(badstrikes)), :]
#Remove butterfly arbitrages
badputs = []
for i=1:size(pre_espss)[1];
for j=i+1:size(pre_espss)[1];
if 2*j - i <= size(pre_espss)[1] && 2*pre_espss.bid[j] - pre_espss.ask[i] - pre_espss.ask[2*j - i] > 0;
push!(badputs, pre_espss.strike[j])
end;
end;
end;
const espss = pre_espss[.!in.(pre_espss.strike, Ref(badputs)), :]
badcalls = []
for i=1:size(pre_escss)[1];
for j=i+1:size(pre_escss)[1];
if 2*j - i <= size(pre_escss)[1] && 2*pre_escss.bid[j] - pre_escss.ask[i] - pre_escss.ask[2*j - i] > 0;
push!(badcalls, pre_escss.strike[j])
end;
end;
end;
const escss = pre_escss[.!in.(pre_escss.strike, Ref(badcalls)), :]
return nothing
Computing the risk-neutral density
While not strictly necessary to simply optimize the position, computing a risk-neutral density is necessary to use the heuristic we devised in the theory section to see just how much better the optimal strategy would be in perfect markets. We don't need anything special, just a quick-and-dirty heuristic, so we'll compute it using typical numerical second-differentiation on bid-ask midpoints, last trade prices for recent enough trades, and last trade prices capped at the bid-ask spread, and compare these to the PDF we'll use with mean shifted to the right place (to give an idea of the shape)
Here's our implementation:
crecent = subset(escalls, :lastTradeDate => d -> d .> DateTime(2024, 9, 17, 15, 17, 30));
clast = max.(min.(crecent.lastPrice, crecent.bid), crecent.ask);
cmid = (crecent.bid .+ crecent.ask)./2
cstr = crecent[:, "strike"];
precent = subset(esputs, :lastTradeDate => d -> d .> DateTime(2024, 9, 17, 15, 17, 30));
plast = max.(min.(precent.lastPrice, precent.bid), precent.ask);
pmid = (precent.bid .+ precent.ask)./2
pstr = precent[:, "strike"];
numdiff(y, x) = [(y[i] - y[i - 1])/(2*(x[i] - x[i - 1])) + (y[i + 1] - y[i])/(2*(x[i + 1] - x[i])) for i=2:length(x)-1]
convolve(y::Vector{Float64}, x::Union{Vector{Int64}, Vector{Float64}}, f::Function) = [sum(y[j]*f(x[j] - x[i]) for j=1:length(y)) for i=1:length(x)]
bothstr = sort(vcat(cstr, setdiff(pstr, cstr)));
bothl = [K in cstr ? (K in pstr ? clast[findfirst(isequal(K), cstr)]/2 + (ess0 - K + plast[findfirst(isequal(K), pstr)])/2 : clast[findfirst(isequal(K), cstr)]) : ess0 - K + plast[findfirst(isequal(K), pstr)] for K in bothstr];
bothl2 = [K < ess0 ? ess0 - K + plast[findfirst(isequal(K), pstr)] : clast[findfirst(isequal(K), cstr)] for K in bothstr];
bothl3 = [K < ess0 ? ess0 - K + pmid[findfirst(isequal(K), pstr)] : cmid[findfirst(isequal(K), cstr)] for K in bothstr];
bfirst = numdiff(bothl, bothstr);
bsecond = numdiff(bfirst, bothstr[2:end-1]);
blinterp = linear_interpolation(bothstr[3:end-2], bsecond);
bfirst2 = numdiff(bothl2, bothstr);
bsecond2 = numdiff(bfirst2, bothstr[2:end-1]);
blinterp2 = linear_interpolation(bothstr[3:end-2], bsecond2);
bfirst3 = numdiff(bothl3, bothstr);
bsecond3 = numdiff(bfirst3, bothstr[2:end-1]);
blinterp3 = linear_interpolation(bothstr[3:end-2], bsecond3);
x = range(0.99, 1.01, length=1000)
plot(x, [blinterp.(x.*ess0).*ess0, blinterp2.(x.*ess0).*ess0, blinterp3.(x.*ess0).*ess0, pdf.(LogNormal(log((disc)^2/sqrt((disc)^2 + 0.00004)), sqrt(log(1 + 0.00004/(disc^2)))), x)]; labels=["capped" "recent" "midpoints" "lognormal"])
savefig("../images/kelly-options/bl1.png")
return nothing
Here are the Breeden-Litzenberger implied PDFs.
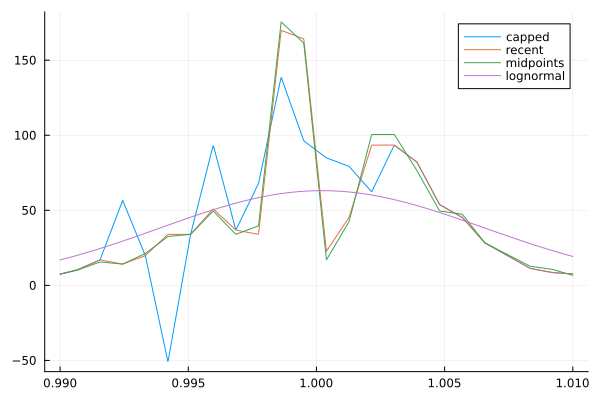
Note that they're bumpy right now, but that's OK, we'll apply Gaussian smoothing later.
dist(s) = pdf(LogNormal(log(disc^2/sqrt(disc + 0.001)), sqrt(log(1 + 0.001/(disc^2)))), s)
gauss(s) = pdf(Normal(0, 0.001), s)/10000
testrange = (bothstr[3]/ess0):0.0001:(bothstr[end-2]/ess0)
plot(testrange, vcat((f -> convolve(dist.(testrange)./(f.(testrange.*ess0).*ess0), collect(testrange), gauss)).([blinterp, blinterp2, blinterp3]), (f -> dist.(testrange)./(f.(testrange.*ess0).*ess0)).([blinterp, blinterp2, blinterp3])); labels=["capped (smoothed)" "recent (smoothed)" "midpoints (smoothed)" "capped" "recent" "midpoints"])
savefig("../images/kelly-options/bl2.png")
return nothing
And here are the solutions to the unconstrained optimization problem based on these risk-neutral densities, smoothed with a bit of Gaussian noise:
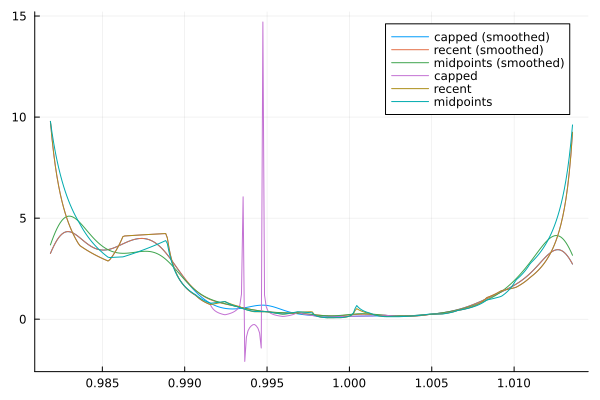
All of these look pretty similar for most of the domain, though the one computed from "capped" last trades looks pretty bad in a low region. We choose to use the bid-ask midpoints because the original Breeden-Litzenberger density looked best, but either of the latter two would have worked fine. Finally, since our example belief PDF gives significant probability that the underlying falls outside the area we could compute by Breeden-Litzenberger, well apply tails from a generalized extreme value (here, Frechet due to fat tails) distribution:
function rtailloss3(params::Vector{Float64})
xi = params[1]
mu = params[2]
sigma = params[3]
return 3*abs(exp(-(1 + xi*(bothstr[end-4] - mu)/sigma)^(-1/xi)) + bfirst3[end-3])^2 +
abs((1/sigma)*(1 + xi*(bothstr[end-4] - mu)/sigma)^(-(xi + 1)/xi)*exp(-(1 + xi*(bothstr[end-4] - mu)/sigma)^(-1/xi)) - bsecond3[end-2])^2 +
abs((1/sigma)*(1 + xi*(bothstr[end-3] - mu)/sigma)^(-(xi + 1)/xi)*exp(-(1 + xi*(bothstr[end-3] - mu)/sigma)^(-1/xi)) - bsecond3[end-1])^2;
#abs((1/sigma)*(1 + xi*(bothstr[end-2] - mu)/sigma)^(-(xi + 1)/xi)*exp(-(1 + xi*(bothstr[end-2] - mu)/sigma)^(-1/xi)) - bsecond3[end])^2;
end
function ltailloss3(params::Vector{Float64})
xi = params[1]
mu = params[2]
sigma = params[3]
return 3*abs(exp(-(1 + xi*(bothstr[end-4] - mu)/sigma)^(-1/xi)) + bfirst3[end-3])^2 +
abs((1/sigma)*(1 + xi*(bothstr[end-4] - mu)/sigma)^(-(xi + 1)/xi)*exp(-(1 + xi*(bothstr[end-4] - mu)/sigma)^(-1/xi)) - bsecond3[end-2])^2 +
abs((1/sigma)*(1 + xi*(bothstr[end-3] - mu)/sigma)^(-(xi + 1)/xi)*exp(-(1 + xi*(bothstr[end-3] - mu)/sigma)^(-1/xi)) - bsecond3[end-1])^2;
end
res = best_candidate(bboptimize(rtailloss3; SearchRange = [(0, 100), (bothstr[1], bothstr[end-4]), (0, 6000)], MaxTime=3, Method = :de_rand_1_bin_radiuslimited));
testrange2 = 5720:0.001:6000
testrange = 1.008:0.0001:(bothstr[end-2]/ess0)
combined3(x) = x > bothstr[end - 3]/ess0 ? (1/res[3])*(1 + res[1]*(x*ess0 - res[2])/res[3])^(-(res[1] + 1)/res[1])*exp(-(1 + res[1]*(x*ess0 - res[2])/res[3])^(-1/res[1])) : blinterp3(x*ess0)
testrange = (bothstr[3]/ess0):0.0001:1.03
plot(testrange, dist.(testrange)./(combined3.(testrange)*ess0))
savefig("../images/kelly-options/bl3.png")
return nothing
And here is the resulting right-extended solution to the unconstrained optimization problem:
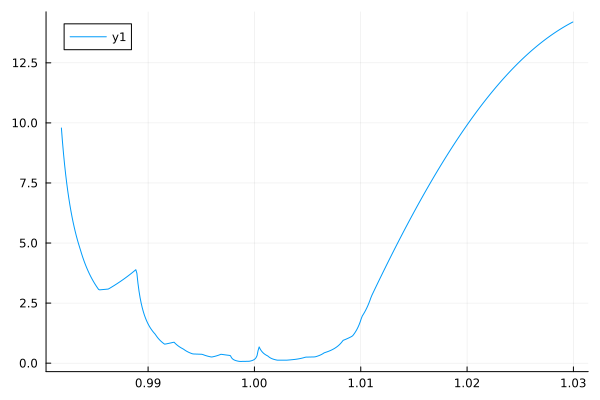
Optimizing Options Positions: Arbitrary Probability Measures
Now, we'll implement an options position optimizer using what we found in the theory section. We'll use numerical integration, which is slow but allows us to use one implementation no matter the choice of \(P\). However, we do need to assume a distribution for testing purposes, so we'll say a lognormal distribution with mean \(1.01\) and variance \(0.001\) (the VIX, which roughly reflects 1-year implied volatility, was about 17 at the time, and these options have only two days until expiry, meaning a lognormal variance of \(\frac{0.17^2}{\sqrt{52*2.5}} \approx 0.0025\), but due to fat tails, if we did not lower the variance further, the directional part would be completely dwarfed by a bet on high variance once we optimized). We "hardcode" this distribution to potentially help the compiler out a bit, as the numerical integration will be pretty slow and we want all the speed we can get. Julia has just-in-time compilation, so this doesn't preclude all flexibility, but it would require a second or two to recompile if we wanted to update our distribution. If we wanted to do this in production, it would be better to pass it (or its parameters) as an argument.
put(k, pr) = (s) -> max(0, k/ess0 - s)/disc - pr/ess0 call(k, pr) = (s) -> max(0, s - k/ess0)/disc - pr/ess0 long = (s) -> s/disc - ess0a/ess0 short = (s) -> - s/disc + ess0b/ess0 const lcalls = call.(escss[:, "strike"], escss[:, "ask"]); const lputs = put.(espss[:, "strike"], espss[:, "ask"]); const sputs = (-).∘put.(espss[:, "strike"], espss[:, "bid"]); const payoff = vcat(lcalls, lputs, sputs, long, short); return nothing
#Proper conversions to log-mean and log-standard deviation
dist(s) = pdf(LogNormal(log(1.01^2/sqrt(1.01^2 + 0.001)), sqrt(log(1 + 0.001/(1.01^2)))), s)
objective(pos::Vector{Float64}) = solve(IntegralProblem.((x, p) -> log(abs(max(2^-1000, (x .|> payoff) ⋅ pos + 1)))*dist(x), 0.2, 3), QuadGKJL()).u
gradient(pos, tightness) = solve(IntegralProblem.((x, p) -> (x .|> payoff).*dist(x)./max(-2^-1000, (x .|> payoff) ⋅ pos + 1), 0.2, 3), QuadGKJL()).u .+ (tightness.*min.(0, pos)).^2
lgrad(pos) = -pos
gradstep = 1600
lagrangestep = 0.1
function optimize(pos, l, firstidx, lastidx)
last = pos;
for j=firstidx:lastidx
#Gradient descent with Nesterov momentum
grad = gradient(pos .+ 0.5*(pos .- last), sqrt(j))
last = pos;
pos += (gradstep/sqrt(j + 1600)).*grad
if j % 50 == 0
@show j
@show objective(pos)
@show minimum(grad)
end
end
return (pos, l)
end
pos = zeros(length(payoff));
l = zeros(length(payoff));
Base.exit_on_sigint(false)
try
(pos, l) = optimize(pos, l, 1, 100)
catch e
if typeof(e) <: InterruptException
println("caught Interrupt")
return 0
end
end
return nothing
(pos, l) = optimize(pos, l, 100, 50000)
x = range(5300, 5800, length=10000)
testrange = (bothstr[3]/ess0):0.0001:1.03
plot([(x, [(x[i]/ess0 .|> payoff) ⋅ pos + 1 for i=1:10000]), (testrange.*ess0, dist.(testrange)./(combined3.(testrange)*ess0))]; ylims=(0, 5), labels=["Real-world position" "\"Perfect market\"-optimal"])
savefig("../images/kelly-options/payoff.png");
return objective(pos)
2.5037119444049063
And here is a graph of the returns of the resulting position (which currently allows arbitrary increments) as a function of the price of the S&P500 index at expiry, compared with the theoretical optimal payoff function based on smoothed bid-ask midpoints (see the information theory part earlier):
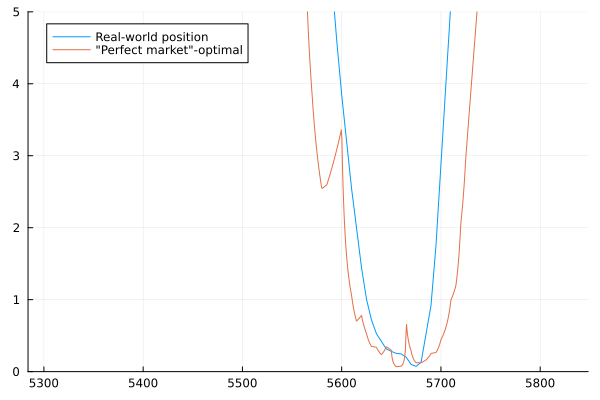
Next, we'll implement a randomized rounding routine to find a solution using real-life contract multiples. To do this, we'll have to assume an initial wealth. Since the contract multiple on these options is \($100\) and the index price is roughly \($5650\), one options contract has a notional value of around \($565,000\), and thus the lowest feasible initial wealth for a trader in options like these is something like \($100,000\), which we'll take as our initial wealth. Note that S&P 500 "mini" options are also offered and have a multiplier of \($10\), meaning an investor with \($10,000\) could apply the same strategy to essentially the same effect (though the bid-ask spreads and/or liquidity might be worse, which would change the optimal strategy slightly. Mini options data doesn't seem to be available on Yahoo finance, though). Also, note that the multiplier is 1 for long/short positions as these can effectively be replicated by a long or short position in an ETF tracking the index.
wealth = 10^5
multiplier = 100
scaledpos(pos) = vcat(pos[1:end-1] .* wealth ./ (ess0 * multiplier), pos[end]*wealth/ess0)
invscaledpos(scaledpos) = vcat(scaledpos[1:end-1] .*(ess0 * multiplier) ./ wealth, scaledpos[end]*ess0/wealth)
best = zeros(length(pos));
bestobj = 0
for i=1:100
candidate = trunc.(scaledpos(pos)) .+ (rand() .<= scaledpos(pos) .% 1)
candidateobj = objective(invscaledpos(candidate))
if candidateobj >= bestobj
best = candidate
bestobj = candidateobj
end
end
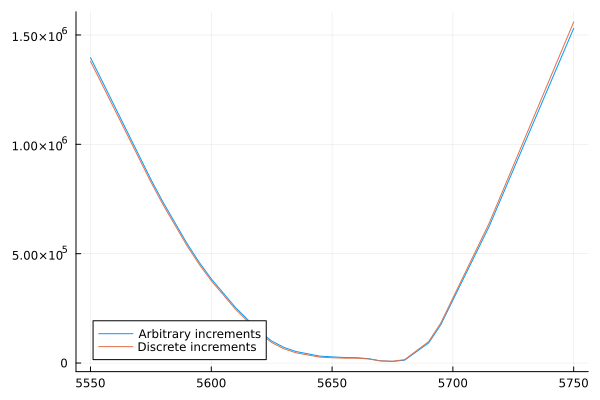
x = range(5550, 5750, length=10000)
plot(x, [[(x[i]/ess0 .|> payoff) ⋅ pos + 1 for i=1:10000], [(x[i]/ess0 .|> payoff) ⋅ invscaledpos(best) + 1 for i=1:10000]].*wealth; label=["Arbitrary increments" "Discrete increments"])
savefig("../images/kelly-options/payoff2.png");
annotationvec = string.("Calls at strike " , escss[:, "strike"] , ": " , best[1:length(escss[:, "strike"])])
append!(annotationvec, string.("Puts at strike " , espss[:, "strike"] , ": " , best[length(escss[:, "strike"]) .+ (1:length(espss[:, "strike"]))] .- best[length(escss[:, "strike"]) .+ length(espss[:, "strike"]) .+ (1:length(espss[:, "strike"]))]))
push!(annotationvec, "Long/short position: " * string(best[end]))
return annotationvec
| Calls at strike 5305: 4.0 |
| Calls at strike 5325: 4.0 |
| Calls at strike 5330: 0.0 |
| Calls at strike 5335: 0.0 |
| Calls at strike 5360: 2.0 |
| Calls at strike 5370: 5.0 |
| Calls at strike 5375: 0.0 |
| Calls at strike 5380: 3.0 |
| Calls at strike 5385: 0.0 |
| Calls at strike 5415: 4.0 |
| Calls at strike 5420: 4.0 |
| Calls at strike 5435: 9.0 |
| Calls at strike 5440: 7.0 |
| Calls at strike 5445: 0.0 |
| Calls at strike 5620: 22.0 |
| Calls at strike 5625: 9.0 |
| Calls at strike 5645: 6.0 |
| Calls at strike 5650: 1.0 |
| Calls at strike 5655: 0.0 |
| Calls at strike 5660: 5.0 |
| Calls at strike 5665: 4.0 |
| Calls at strike 5670: 8.0 |
| Calls at strike 5675: 17.0 |
| Calls at strike 5680: 33.0 |
| Calls at strike 5690: 52.0 |
| Calls at strike 5695: 58.0 |
| Puts at strike 5575: 15.0 |
| Puts at strike 5580: 17.0 |
| Puts at strike 5590: 20.0 |
| Puts at strike 5595: 19.0 |
| Puts at strike 5600: 20.0 |
| Puts at strike 5610: 21.0 |
| Puts at strike 5625: 21.0 |
| Puts at strike 5630: 20.0 |
| Puts at strike 5635: 17.0 |
| Puts at strike 5645: 9.0 |
| Puts at strike 5655: 4.0 |
| Puts at strike 5660: -12.0 |
| Puts at strike 5665: -15.0 |
| Puts at strike 5670: 7.0 |
| Puts at strike 5680: 36.0 |
| Puts at strike 5690: 35.0 |
| Puts at strike 5715: 35.0 |
| Puts at strike 5720: 0.0 |
| Puts at strike 5730: 0.0 |
| Puts at strike 5760: 0.0 |
| Puts at strike 5770: 22.0 |
| Puts at strike 5780: 25.0 |
| Puts at strike 5810: 0.0 |
| Puts at strike 5875: -35.0 |
| Puts at strike 6000: -8.0 |
| Puts at strike 6100: -10.0 |
| Long/short position: 0.0 |
Finally, here's a chart comparing the returns of the rounded position and the original position (observe that the rounded position is extremely close):
Speed Limitations and an Analytical Approximation
In practice, this exact algorithm is likely to be unusably slow in production because of the required numerical integration, requiring a few minutes to converge on a Ryzen 5900H. Newton's method also won't help: our bottleneck here is computing numerical integrals in each entry of the gradient or Hessian, not inverting the Hessian, and we'd have to compute the same number of those numerical integrals for the same theoretical convergence guarantees. Quasi-Newton methods might get us into the territory of seconds, but at the cost of possibly failing to converge depending on \(\frac{dP}{dm}\) – that would be bad in production, too! However, if we had an analytical gradient or Hessian, the algorithm would be orders of magnitude faster, likely converging in milliseconds.
Unfortunately, for most parametric families we would want to use, computing the gradient or Hessian analytically is a fairly difficult task, and some families may not even admit a closed-form representation. Let's go into some details of how one might proceed.
First, we can deal with the piecewise nature of the payoff functions by breaking up the domain into intervals between strike prices. Within such intervals the payoff is a linear function of the position. In particular, if \(K_1, K_2\) are strikes with no intermediate strikes between them, then on \((K_1, K_2)\) we have
\begin{align*} \hat{\alpha} \cdot \hat{C}(S_1) + \hat{\beta} \cdot \hat{P}(S_1) + \check{\beta} \cdot \check{P}(S_1) + 1 &= \\ &S_1 \left( \sum_{\substack{K \in E \\ K > K_1}} \left( \check{\beta}_K - \hat{\beta}_K \right) + \sum_{\substack{K \in E \\ K \leq K_1}} \hat{\alpha} \right) e^{-rt} \\ &+ \left(\sum_{\substack{K \in E \\ K > K_1}} \left( \hat{\beta}_K K - \check{\beta}_K K \right) - \sum_{\substack{K \in E \\ K \leq K_1}} \hat{\alpha}_K K \right) e^{-rt} \\ &+ \hat{\beta} \cdot \hat{P}(\infty) + \check{\beta} \cdot \check{P}(\infty) + \hat{\alpha} \cdot \hat{C}(0) + 1 \end{align*}which means the inside of the log (in the objective function), the denominator (in the gradient), or the square root of the denominator (in the Hessian) can be written as \(ax + b\) on such intervals, greatly simplifying them. Thus for arbitrary \(P\), the extent of the calculus we need to do is finding the antiderivatives of \[ \frac{dP}{dm} (x) \log( \vert ax + b \vert ) \] for the objective function, \[ x \frac{dP}{dm} (x) \frac{1}{ax + b} \] and \[ \frac{dP}{dm} (x) \frac{1}{ax + b} \] for the gradient, and
\begin{align*} x^2 &\frac{dP}{dm} (x) \frac{1}{(ax + b)^2}, \\ x &\frac{dP}{dm} (x) \frac{1}{(ax + b)^2}, \\ &\frac{dP}{dm} (x) \frac{1}{(ax + b)^2} \\ \end{align*}for the Hessian. Any of these groups of antiderivatives would give a major speedup (even an analytical Hessian with a numerical gradient would be a big improvement), and it may turn out that some are easier than others. But even if we only had a closed-form antiderivative for the objective function, we could probably find closed-form gradients and Hessians with symbolic differentiation software packages, and approximating them numerically would also be feasible as the objective function is fairly smooth in the feasible region. So our main focus will be on finding \[ \int_0^x \frac{dP}{dm} (y) \log( \vert ay + b \vert ) \mathop{dm(y)}.\]
This seems fairly straightforward when written this way, but let's consider what \(\frac{dP}{dm}\) actually is. Most plausible distributions that could model stock returns are the exponent of some roughly symmetric distribution with mean 0. In the case of our toy example with lognormal returns with mean 1.04 and variance 0.004, the density function is something like \[\frac{dP}{dm}(x) = \frac{\exp\left(- \frac{(\log(x) - 0.026036)^2}{0.0263689}\right)}{\left(0.162385x \sqrt{2\pi}\right)}.\]
This results in integrals like
\begin{align*} \int_{0}^{x} \frac{\exp \left(- \frac{(\log(y) - c)^2}{d}\right)}{y} \log( \vert ay + b \vert ) \mathop{dm(y)} \\ = \int_{0}^{x} e^{\frac{-c^2}{d}} y^\left(\frac{-\log(y) + 2c}{d} - 1 \right) \log( \vert ay + b \vert ) \mathop{dm(y)} \end{align*}even for our "toy" example, which are highly nontrivial. SymPy and several other symbolic and symbolic-numeric integrators seem to agree, and either error out or return an expression that still contains an integral. Thus, a direct analytical solution and implementation is out of scope for this article.
However, astute readers may recognize that even if a direct solution is impossible, polynomial approximations of \(\frac{dP}{dm}\) should result in integrals that are more or less trivial if used in place of \(\frac{dP}{dm}\), and thus we can (analytically) approximate the objective function, gradient, etc by their Taylor series assuming these are analytic in the appropriate interval. In our toy example, aside from perhaps cases where a denominator or parameter of log is zero in an interval (which will never occur in a feasible region by proofs in earlier sections, though might occur in practice depending on the optimization routine), the integrand is clearly smooth with bounded derivatives over intervals between strikes, so its integral, regardless of whether it has a closed-form expression, also has this property (by the fundamental theorem of calculus) and is thus analytic over such intervals between strikes.
This wouldn't actually change the results from our earlier numerical integration: QuadGKJL, the Gauss-Kronrod quadrature we used, is approximating the integrals based on a slightly more complicated version of the same idea under the hood. However, it could save time because QuadGKJL doesn't know that the terms of the Taylor series will be of the same parametric form each time, just with different coefficients, but we do know this and thus could hard-code it into our own quadrature method. We won't give a second implementation using this idea as it would be somewhat involved, but anyone who might want to implement this for a real-world purpose might benefit from it.
Conclusion, and Towards Parametric Models
The fact that optimizing the expected log returns is numerically tractable for slower investment styles even for non-parametric \(p\), at least on timescales of seconds (though short of the microseconds required by high-frequency traders), is promising for its use among e.g. fundamental analysts and earnings traders, who might have an idea of pricing at expiry but lack complicated, regression-fit models of options prices over time. But even these traders generally have some idea of when price events will happen, and it doesn't always cleanly coincide with option expiry dates. In fact, if we're willing to start using parametric price models over time, can trade calendar/horizontal spreads, and allow some intertemporal hedging, the extra information and expressiveness can allow us to do much better than this. In the interest of getting this article out now, this material can't all be covered at once, but I have plans to cover these questions in a later article when I get the chance.
Footnotes:
The definition of completeness used by most other authors is that all such contingent claims are constructible using some admissible trading strategy, in particular one that can trade at intermediate times, but for our purposes (we'll only trade at times \(t\) and \(T\) in this article), there's no practical difference. When I get around to writing the next part (which will use horizontal spreads), though, I might have to amend this.
To be technically precise, we need the stricter condition of no free lunch with vanishing risk, though if we only allow trading at times \(t\) and \(T\) (we will only use trades of this type in this article), this is equivalent to being arbitrage-free.
To see this, suppose \(Q_T\) is an equivalent martingale measure on \((\Omega, \mathcal{F}_T)\) (one must exist by the first fundamental theorem of asset pricing). Since \[ C^{(0, T)}_K(S_T) = e^{-rT} (S_T - K)^+ + C^{(0, T)}_K (0) \] is a \(Q_T-\)martingale, we have \[0 = \mathbb{E}^{Q_T} \left[ e^{-rT}(S_T - K)^+ + C^{(0, T)}_K (0) \right] \] and thus \[ C_K^{(0, T)} (0) = -\int_0^\infty e^{-rT}(S_T - K)^+ \mathop{dQ_T} = -\int_0^\infty e^{-rT} (x - K)^+ \frac{dQ_T(S_T^{-1})}{dm}(x) \mathop{dm(x)}, \] with \(m\) the Lebesgue measure (so \(\frac{dQ_T(S_T^{-1})}{dm}\) is \(S_T\)'s probability density function under \(Q_T\) with respect to \(m\)). Taking the second derivative of both sides with respect to \(K\), we obtain that \[ \frac{d^2C_K^{(0, T)(0)}}{dK^2} = e^{-rT} \frac{d}{dK} \int_K^\infty \frac{dQ_T(S_T^{-1})}{dm}(x) \mathop{dm(x)} = -e^{-rT} \frac{dQ_T(S_T^{-1})}{dm}(x) \quad \text{a.s.}\] and thus \[ \frac{dQ_T(S_T^{-1})}{dm}(x) = -e^{rT} \frac{d^2C^{(0, T)}_K(0)}{dK^2} \quad \text{a.s..} \]
Though the distinction doesn't matter for this article, one could argue that \(Q_T\) is "dictated" by the "odds", and not the other way around, given how we found \(Q_T\). This is in some sense true, but what causes the "odds" to be set the way they are, then? We won't go into detail here, but they can be interpreted as a function of the "market consensus" underlying probability measure, say \(R_T\), and the "stochastic discount factor" \(\frac{dQ_T}{dR_t}\), which can be interpreted as a sort of "market consensus" utility preference. While it's not possible to totally disentangle these (so changes in valuation could be attributed to changes in either) and so they can't be empirically observed, the view that \(R_T\) and \(\frac{dQ_T}{dR_T}\) set derivative prices and not the other way around offers more attribution to the motives of market participants, allowing us to assume they act rationally and systematically.
If we had used other isoelastic functions instead of log, one might anticipate that we would end up with the Renyi divergence. However, because the expectation is still taken with respect to \(P\) rather than \(R\), and Renyi divergence does not satisfy the chain rule of entropy in the same way, we actually get a somewhat different quantity. See Soklakov 2018 for more details, which also covers a lot of the same ground as this section.
On options with very near expiry dates, this might actually be false. For example, most exchanges will halt trading on a particular stock if its value rises more than a certain percentage within a single day, so \(P\) will have bounded support on such timescales. However, we won't consider this case here.